home blog search about
◐

forward chaining

forward and backward chaining for algorithmic inference2023-09-19

(Peter Norvig, Stuart J. Russell, 2020 section 7.5.4)
a family of inference algorithms

propositional logic chaining

the forward-chaining algorithm (which stands for "propositional logic forward chaining entails" and is shown in fig-forward-chaining-2) determines if a single proposition symbol –the query–is entailed by a knowledge base of definite clauses. it begins from known facts (positive literals) in the knowledge base. if all the premises of an implication are known, then its conclusion is added to the set of known facts. for example, if and are known and is in the knowledge base, then can be added. this process continues until the query is added or until no further inferences can be made. it is important to remember that this algorithm runs in linear time.
the best way to understand the algorithm is through an example and a picture. fig-forward-chaining-1 shows a simple knowledge base of horn clauses with and as known facts and the knowledge base drawn as an graph.
in graphs, multiple edges joined by an arc indicate a conjunction-—every edge must be proved—-while multiple edges without an arc indicate a disjunction—-any edge can be proved. it is easy to see how forward chaining works in the graph. the known leaves (here, and ) are set, and inference propagates up the graph as far as possible. wherever a conjunction appears, the propagation waits until all the conjuncts are known before proceeding.

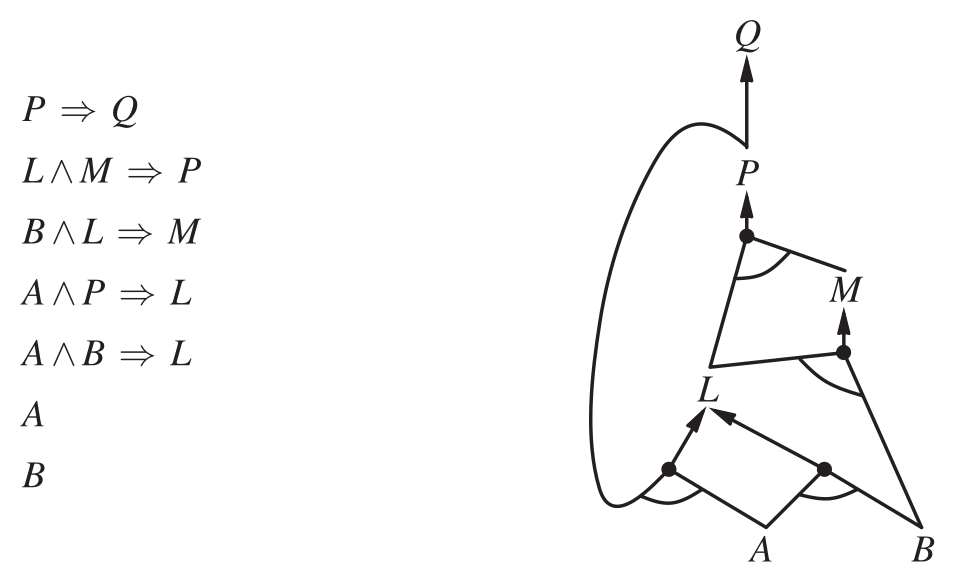
a set of horn clauses and the corresponding graph

in tikz:

although this graph drawing isnt as informative, as we cant tell if an arrow is part of a disjunction or a conjunction, perhaps we could color arrows or something? as drawing angles properly like in fig-forward-chaining-1 would be much more complex, we could also insert intermediate nodes that represent AND and OR which arrows would have to to go through if they're part of an AND or an OR (each statement would require its unique connective node in the graph).

forward chaining algorithm for propositional logic

the backward chaining algorithm, as its name suggests, works backward from the query. if the query is known to be true, then no work is needed. otherwise, the algorithm finds those implications in the knowledge base whose conclusion is . if all the premises of one of those implications can be proved true (by backward chaining), then is true. when applied to the query in fig-forward-chaining-1, it works back down the graph until it reaches a set of known facts, and , that forms the basis for a proof. as with forward chaining, an efficient implementation runs in linear time.

first-order logic chaining

fig-forward-chaining-3 shows a simple forward chaining inference algorithm for first-order logic. starting from the known facts, it triggers all the rules whose premises are satisfied, adding their conclusions to the known facts. the process repeats until the query is answered (assuming that just one answer is required) or no new facts are added. notice that a fact is not "new" if it is just a renaming of a known fact—-a sentence is a renaming of another if they are identical except for the names of the variables. for example, and are renamings of each other. they both mean the same thing: "everyone likes ice cream."

a conceptually straightforward, but inefficient, forward-chaining algorithm. on each iteration, it adds to KB all the atomic sentences that can be inferred in one step from the implication sentences and the atomic sentences already in KB. the function replaces all variables in its arguments with new ones that have not been used before.

the law says that it is a crime for an American to sell weapons to hostile nations. the country Nono, an enemy of America, has some missiles, and all of its missiles were sold to it by Colonel West, who is American.

first, we will represent these facts as first-order definite clauses:
"…it is a crime for an American to sell weapons to hostile nations":

"Nono…has some missiles." the sentence is transformed into two definite clauses by existential instantiation, introducing a new constant :

"all of its missiles were sold to it by Colonel West":

we will also need to know that missiles are weapons:

and we must know that an enemy of America counts as "hostile":

"West, who is American…":

"the country Nono, an enemy of America…":

we use this crime problem to illustrate . the implication sentences available for chaining are eq-forward-chaining-1, eq-forward-chaining-2, eq-forward-chaining-3 and eq-forward-chaining-4, the algorithm finishes after 2 iterations and we get the proof tree illustrated in fig-forward-chaining-4:

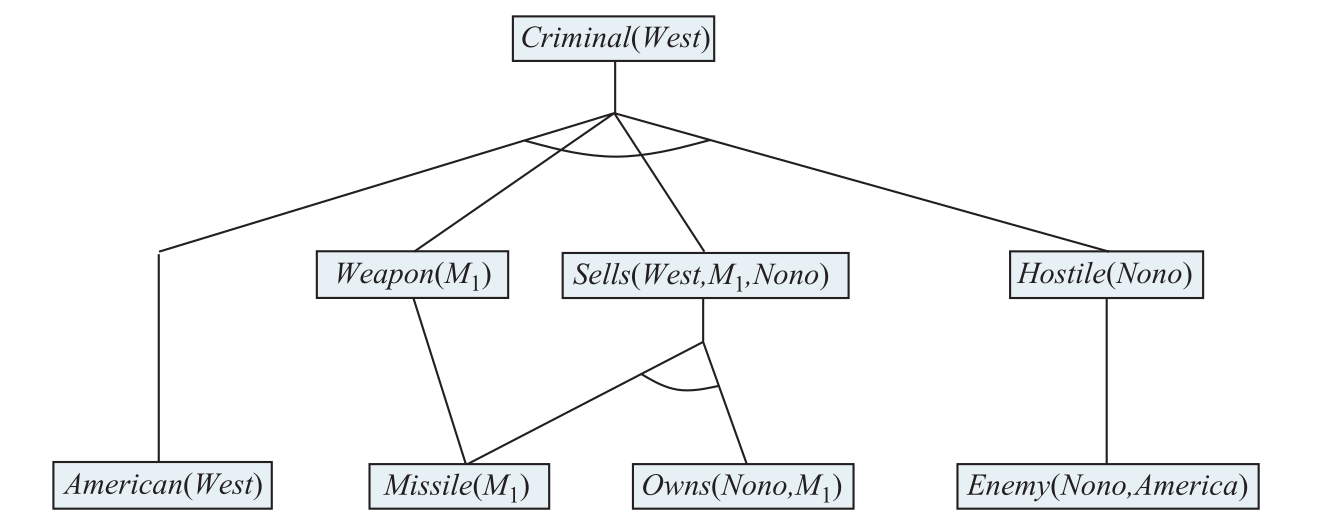
and-or tree of the solution for the example

the [BROKEN LINK: alg-1] in the algorithm was written very vaguely, there is considerable complexity to it on its own.
first, which values are eligible for the variable (the substitution) at the [BROKEN LINK: alg-1]? in other words, what is the domain of ? and how do we generate those values? well, the general form for a substitution is , so with variables and constants in a knowledge base, we need to find all variable combinations of length 1 to , such that order doesnt matter and repetition isnt allowed, order shouldnt matter because (for example) the substitutions and have the same effect, so theres no point in considering both cases, and the repetition of variables shouldnt be allowed because we cant have cases like where a variable gets substituted by multiple values. the total number of variable combinations would be . finally, we should also consider the empty substitution, .
for each combination of variables we need to generate all variations of constants such that repetition is allowed and order matters, repetition should be allowed because different variables shuold be able to hold the same constant value, and order should matter because it matters which variable gets substituted by which constant value. the total number of variations for a combination of variables of length is . the total number of possible substitutions is .
the candidates for the expression in form variations and we need to generate those aswell for each candidate substitution, because such premises-- –are stored individually in the knowledge base.

fig-forward-chaining-4 shows a backward-chaining algorithm for definite clauses. will be proved if the knowledge base contains a rule of the form , where lhs (left-hand side) is a list of conjuncts. an atomic fact like is considered as a clause whose lhs is the empty list. now a query that contains variables might be proved in multiple ways. for example, the query could be proved with the substitution as well as with . so we implement as a generator—-a function that returns multiple times, each time giving one possible result.
works by fetching all clauses that might unify with the goal, standardizing the variables in the clause to be brand new variables, and then, if the of the clause does indeed unify with the goal, proving every conjunct in the , using . that function works by proving each of the conjuncts in turn, keeping track of the accumulated substitution as it goes.
backward chaining, as we have written it, is clearly a depth-first search algorithm. this means that its space requirements are linear in the size of the proof. it also means that backward chaining (unlike forward chaining) suffers from problems with repeated states and incompleteness. despite these limitations, backward chaining has proven to be popular and effective in logic programming languages.

backward chaining algorithm for first-order logic