depth-first search is an algorithm for traversing graphs.
dfs starts at an arbitrary vertex and progresses from neighbor to neighbor.
a free vertex is one that hasnt yet been visited
during the traversal, two timestamps are set for each vertex, discovery timestamp and departure timestamp, each timestamp is a number between 1 and . each such number corresponds to only one timestamp, the timestamps are stored in the following variables:
- discovery time: which is set when is first visited during the traversal
- departure time: which is set when is last departured
next to each vertex is its discovery/departure timestamps
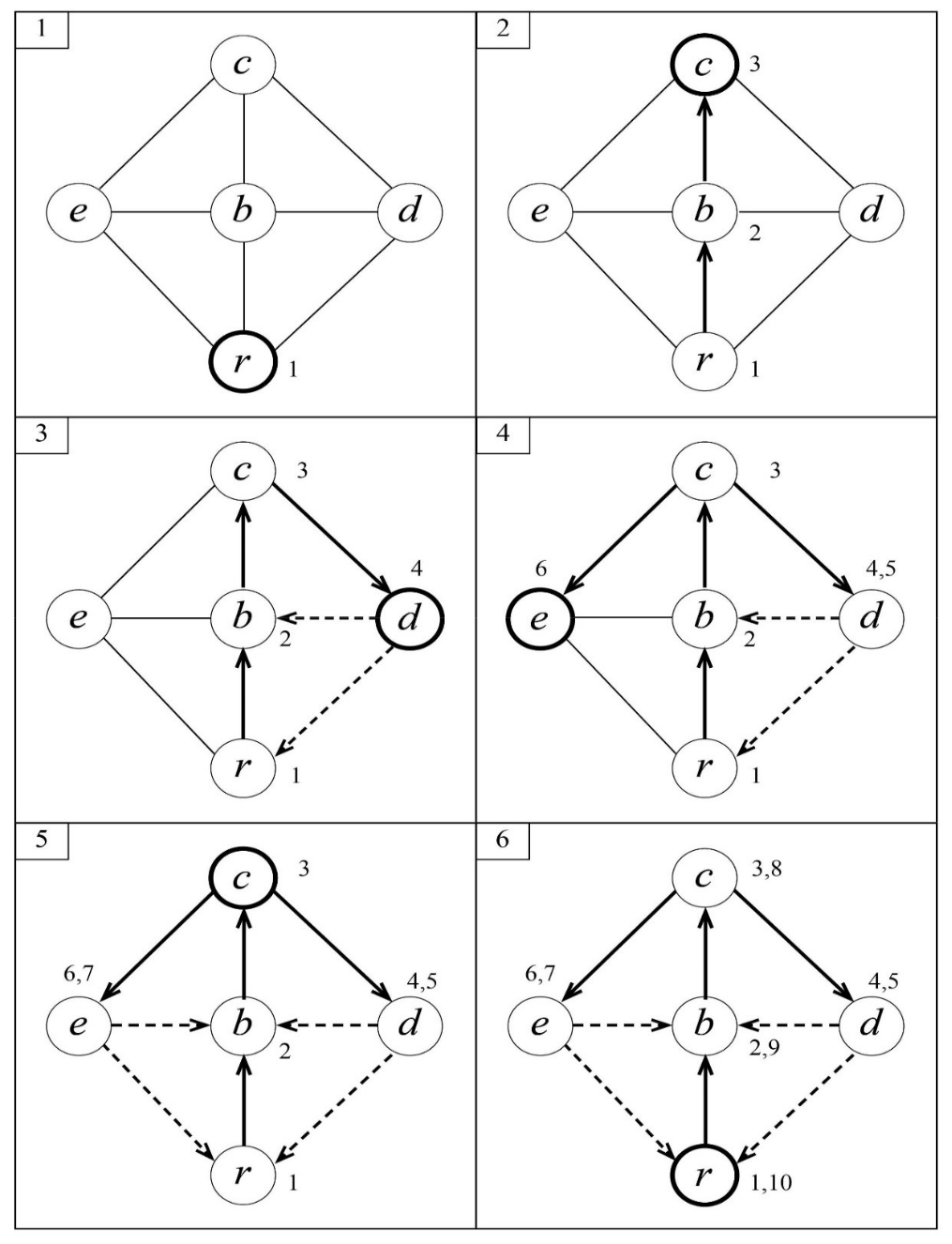
Figure 1: an example of dfs execution
a dfs tree gets built during traversal, if we're at a vertex and we wanna move to vertex , then:
- if is free, we move to and the edge is a tree edge, and is included in the dfs tree
- if isnt free, we dont move to . in this case, the edge is called a back edge in the sense that its directed from to and . isnt included in the dfs forest
process of a visit
let be a free vertex, say we're moving from the vertex to . before we move to , is marked as the vertex previous to .
when we are at , at the beginning of the visit, we mark as a non-free vertex. then we go through each neighbor of one after another, skipping any neighbors that are marked as non-free.
assume that the neighbor vertex is free: we mark as the parent of , we timestamp the visit in and start our visit at . after we're done with , we retreat to , and renew our visit at .
when we've gone through all of 's neighbors, we're done with our visit at , we retreat to .
when we finally retreat to the origin node and there's no more free vertices, the first output tree would be complete. the process is over when there's no vertices left non-visited.
the simplest way to implement this logic is using recursion, which we may see later in the function.
data structures used
the data structures used in the dfs algorithm are
- a global variable that allows giving timestampts to each call. the initial value of is 1.
- for every vertex
we define 3 variables:
- : the discovery time of (value of at the start of )
- : the departure time of (the value of at the end of )
- : the preceding node to in the output tree
pseudocode
the function initiates the data structures we need, traversal is done by
further analysis
the total time complexity of the dfs algorithm is
complexity of is .
for each , the function is executed exactly one time. the complexity of this function is equal to the number of neighbors of .
let be a connected undirected graph in which has been applied. for each vertex :
- the function is executed once only
assume is an edge in an undirected graph . if is a tree edge and , then is directed from to
let and be neighboring vertices in (that dfs is being applied to). if is free at time then is a descendant of in
let be a graph that dfs is being applied to. the vertex is a descendant of a vertex in iff at time in graph there is a path of free nodes from to
let be an undirected connected graph that dfs has been applied to starting at the vertex . then contains a single rooted tree whose root is
let be an undirected connected graph. assume that was applied to . for each edge , is either a tree edge or a back edge.
dfs in a directed graph
its not much different from dfs being applied to an undirected graph except that during traversal we only jump to neighbors that are descendants
an edge is a forward edge if is an ancestor of in .
if is a forward edge directed from to , then if is a cross edge directed from to then
topological sorting
proof of correctness: assume that is an edge in that is directed from to . if we were to apply to , then .
time complexity: same as dfs,