tree data structure

a tree is an abstract data type which stores data in the shape of a downwards-growing tree and every entry is called a node

node

trees store data as nodes, meaning each item in a tree is called a node

each node x has the following fields

key(x): a key that's used to identify the node (like every data structure)
info(x): contains the data we need to store (like every data structure)
left(x): a pointer to the left child of x
right(x): a pointer to the right child
parent(x) (optional): a pointer to the parent of x

every node in a binary tree has from 0 to 2 children

height

the height of a node x is defined as the height of subtree of said node, denoted by

balance factor

the balance factor of a node x, denoted by balance(x) or BF(x), is defined as the height of the subtree of the left child of x, denoted by minus the height of the subtree of the right child of x denoted by , in short: see for example this tree, the balance factor of each node is written above it

height

the height of a tree is the number of the nodes in the longest path downwards (including the root node)

level

the level of a row in the tree is its distance from the root whose level is 1

root

the tree itself T (not every node) contains a pointer root(T) that points to the root node of the tree (the first and topmost node).

leaf

a node that doesnt have children is called a leaf

internal node

a node that has atleast one child is called an internal node

sibling

2 nodes are considered siblings if they share the same parent node

ancestor

an ancestor of a given node is a node that is at an upper level of it

descendant

a descendant of a given node is a node that is at a lower level of the given node

subtree

for some binary tree T and a node x of said tree we denote as the subtree whose root is x, and the left subtree of x is the tree whose root is the left child of x denoted by and the right subtree of x is the tree whose root is the right child of x denoted by

the height of this tree is 4

complete tree

a complete binary tree is a binary tree in which every node has 2 or 0 children, and the leaves are all on at the same level

almost complete tree

an almost complete binary tree is a binary tree from which 0 or more nodes have been deleted continuously from the right part of the last level of nodes

the nodes in the last level in an almost complete binary tree have to appear continuously from left to right

every complete tree is an almost complete tree but not every almost complete tree is a complete tree

every level contains 2 times as many nodes as the level before it, except perhaps for the last level

the height of a tree is

the number of nodes in a tree is

the number of nodes at height is

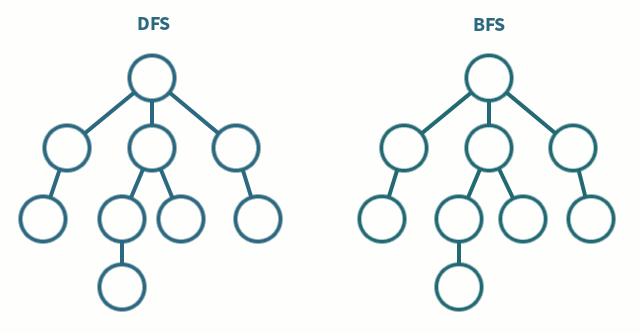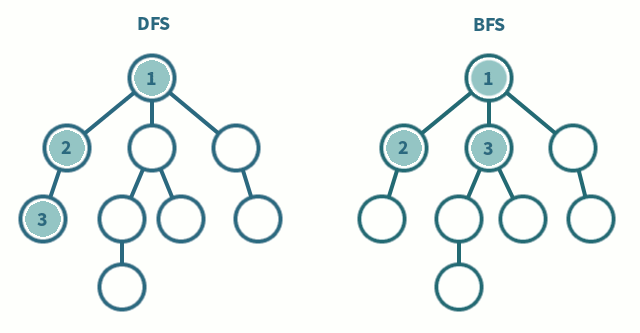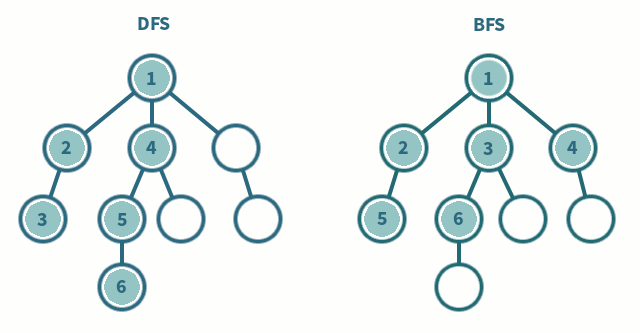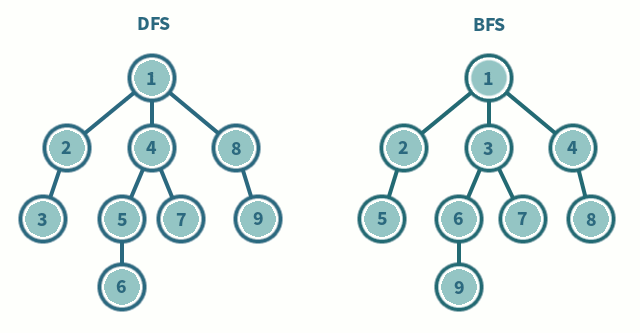
tree breadth-first search

breadth-first search or BFS for short, explores each level before moving onto the next one extra memory, usually a queue, is needed to keep track of the child nodes that were encountered but not yet explored.

tree depth-first search

depth-first search or DFS for short, consists of exploring branches as far as possible before backtracking and exploring branches of other nodes this is the algorithm we'll be using because its simpler

inorder traversal

left, parent, right

Algorithm inorder(tree)
  1. go to the left child, i.e., call inorder(left-child), print it
  2. go back to the parent, print it
  3. go to the right child, i.e., call inorder(right-child), print it

note that before printing a child will always call inorder(left-child), so the first node to print would be the leftmost node in the deepest level

preorder traversal

parent, left, right

Algorithm preorder(tree)
  1. visit the parent, print it
  2. go to the left child, i.e., call preorder(left-child), print it
  3. go to the right child, i.e., call preorder(right-child), print it

postorder traversal

left, right, parent

Algorithm postorder(tree)
  1. go to the left child, i.e., call postorder(left-child), print it
  2. go to the right child, i.e., call postorder(right-child), print it
  3. visit the parent, print it

algorithms

reverse inorder

given a binary tree, write a function to reverse its inorder traversal output

this algorithm runs in O(n) time

template <typename T>
void reverse(BinaryTreeNode<T>* node) {
  if (node == nullptr)
    return;
  reverse(node->get_left());
  reverse(node->get_right());
  BinaryTreeNode<T>* l = node->get_left();
  node->set_left(node->get_right());
  node->set_right(l);
}

example usage:

#include <iostream>




int main() {
  BinarySearchTree<int> t;
  t.insert(11)->insert(5)->insert(3)->insert(4)->insert(2)->insert(1)->insert(7)->insert(6)->insert(20)->insert(15);
  t.print();
  reverse(t.get_root());
  t.print();
}

1	2	3	4	5	6	7	11	15	20
20	15	11	7	6	5	4	3	2	1