graph cycle

if is a path and , then the graph is called a cycle.

a cycle is a simple cycle if it has no repeated vertices except the beginning and the end.

a non-empty sequence of darts is a walk if the head of is the tail of for every . to be more specific, it is a -to- walk if is or the tail of and is or the head of . we define the successor of in to be and we define predecessor of to be . we may designate a walk to be a closed walk if the tail of is the head of , in which case we define the successor of to be and the predecesor of to be . we also refer to a closed walk as a tour.

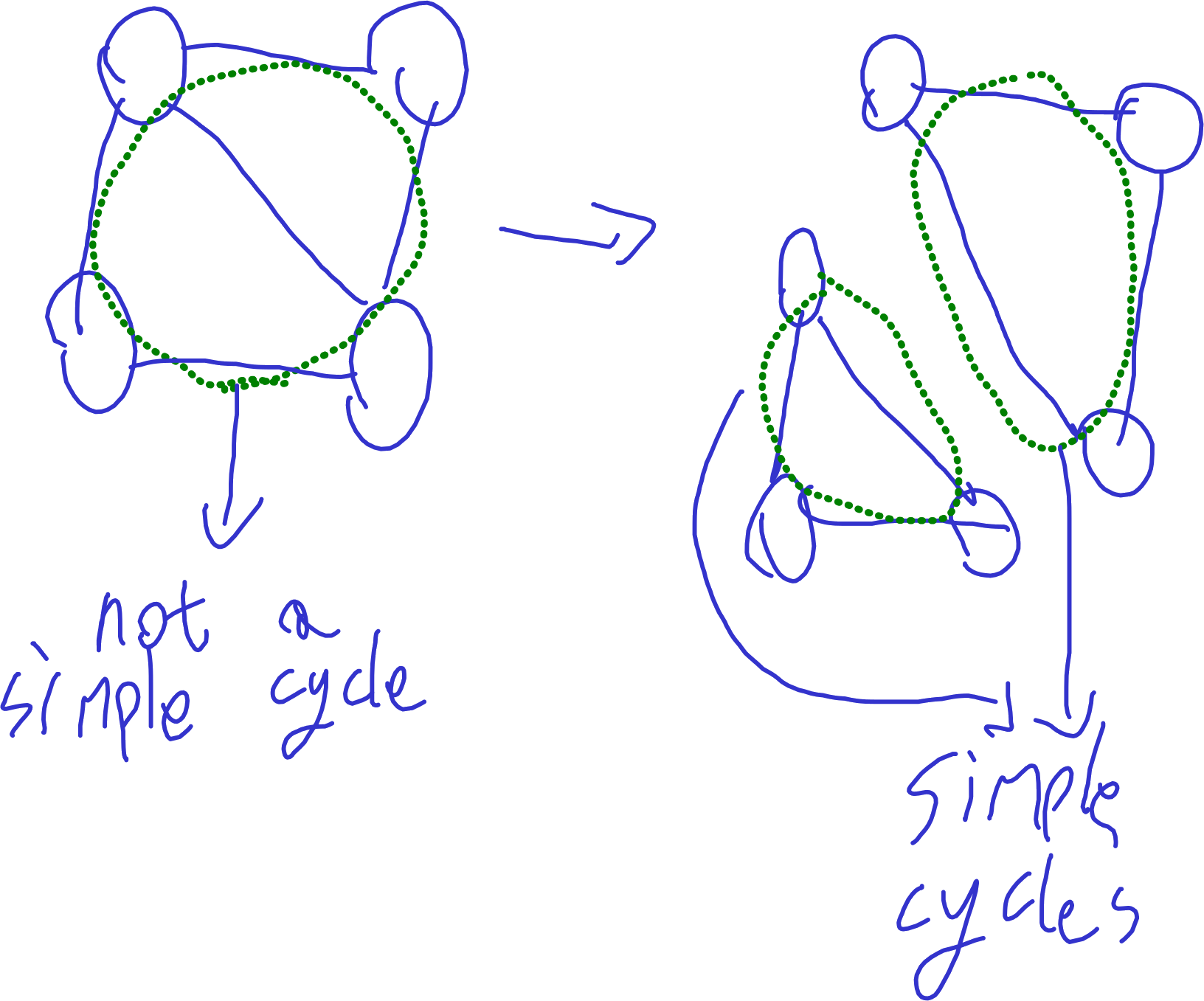
a walk is called a path of darts if the darts are distinct, a cycle of darts if in addition it is a closed walk. a path/cycle of darts is called a path/cycle of arcs if each dart is of the form . it is called a path/cycle of edges if no edge is represented twice.

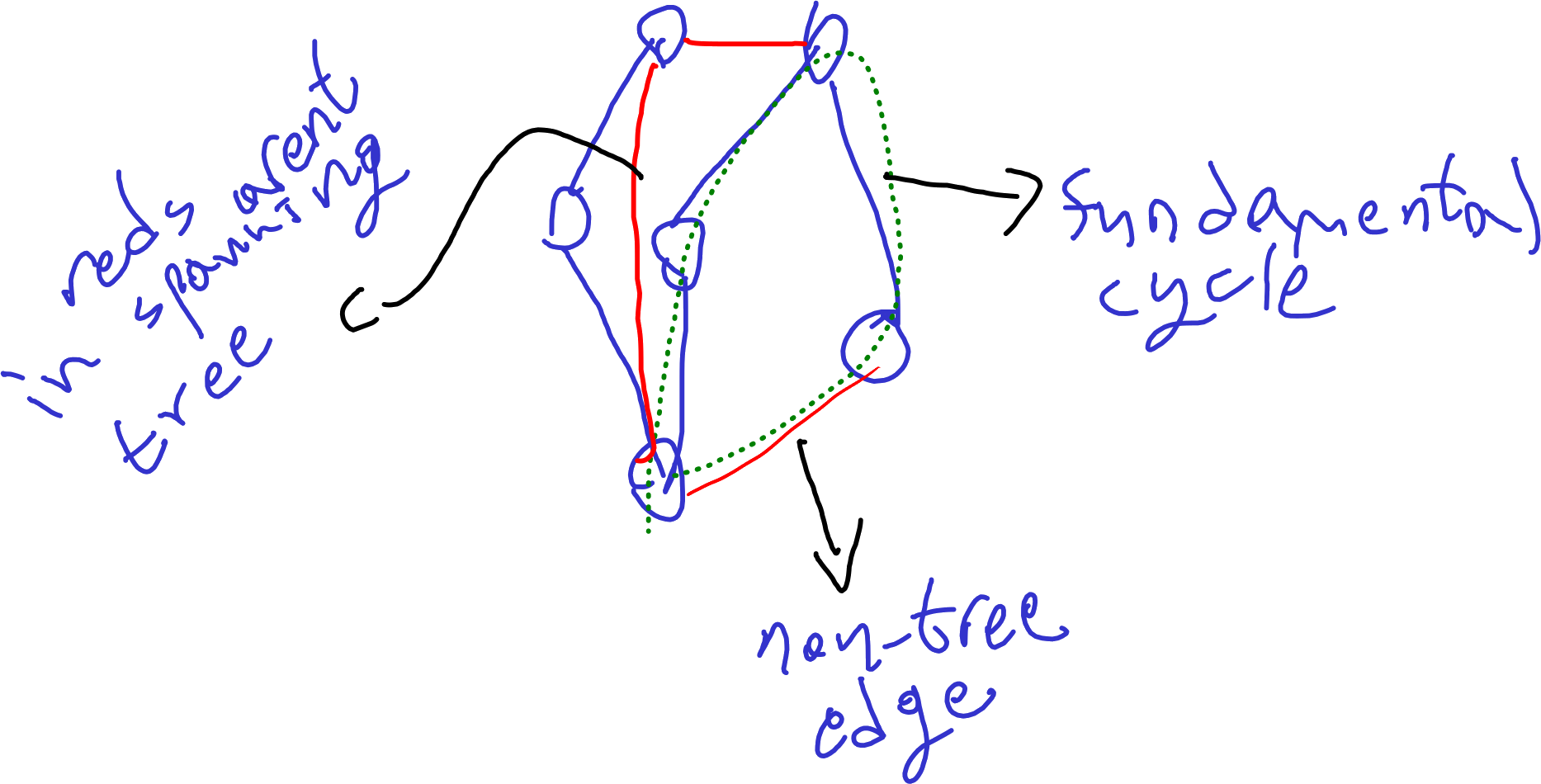
let be a graph, and let be a spanning forest of . for a dart of an nontree edge, there is a simple head( )-to-tail( ) path of darts in whose edges belong to . write so is a simple cycle of darts, called the fundamental cycle of with respect to . for an arc of , we define the fundamental cycle of to be the fundamental cycle of the primary dart .

let be a simple cycle of darts in a connected plane graph . let be an arbitrary face, designated the infinite face. we say the cycle encloses a face with respect to if where .