the following definition is an edge-centric definition of graphs, in which edges are primary and vertices are defined in terms of edges.
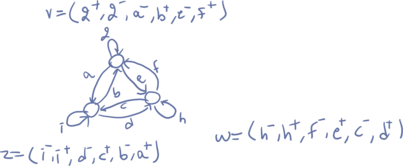
for any finite set , a graph on is a pair where is a partition of the set , called the dart set of . that is, is a collection of disjoint, nonempty, mutually exhaustive subsets of . each subset is a vertex of . for any , the darts of are the pairs and , of which the primary dart of is . for brevity, we can write as and as .
the head of a dart is the block such that contains . the tail of is the head of . note that this isnt exactly synonymous with edge direction, an edge can be directed towards but we can have a dart whose head is (when we have ).
there is one seeming disadvantage: this definition of graphs does not permit the existence of isolated vertices, vertices with no incident edges. this disadvantage is mitigated by interpreting a subset of edges of a graph as a kind of subgraph.
define the bijection rev on darts by . for a dart , is called the reverse of .
the terminology dart reverse may be deceiving, consider the edges , their corresponding darts are , we have that but because .
Let be a graph. the dart space of is , the set of vectors a that assign a real number to each dart . for a vector in dart space and given a set of darts, denotes .
the vertex space of is . a vector of vertex space is called a vertex vector.
the arc space of is a vector subspace of the dart space, namely the set of vectors in the dart space that satisfy antisymmetry: a vector in arc space is called an arc vector.
for a dart , define to be the arc vector such that and for all darts such that and . we extend this notation to sets of darts: .
formally, a vertex is the set of darts having as head, so where the sum is over those darts whose heads are .
for a graph , we denote by the dart-vertex incidence matrix, the matrix whose columns are the vectors . that is, has a row for each dart and a column for each vertex , and the entry is 1 if is the head of if is the tail of , and zero otherwise.