AVL tree

an AVL tree is a binary search tree in which every node x has a balance factor of , meaning: every node x of this tree holds an extra field called balance which holds the balance factor of said node for example, the following tree is an AVL tree:

if we were to remove the node with value 14 or with value 9 this wouldnt be an AVL tree

let T be an AVL tree with n nodes and height , then

minimal form

a minimal form of an AVL tree with a given height is one which contains the least possible number of nodes

the minimal number of nodes for a tree of height is given by the following recurrence relation

according to some sources, the base cases are , but the base cases given above make more sense because a tree with a single node should have a height of 1 not 0

a minimal form of an AVL tree with a given number of nodes is the one with the smallest height which is given by:

here is a python snippet to find the minimal number of nodes needed for a given height:

def find(height):
  if height == 1:
    return 1
  if height == 2:
    return 2
  return find(height-1) + find(height-2) + 1
return [(i,find(i)) for i in range(1,15)]

height	nodes
1	1
2	2
3	4
4	7
5	12
6	20
7	33
8	54
9	88
10	143
11	232
12	376
13	609
14	986

problematic node

a problematic node is a node whose balance factor is

insertion

the process of inserting a node to an AVL tree starts with inserting it using the same insertion method we used for a binary search tree, after said insertion we start going up the tree starting at the new node we just inserted and updating the balance factor for every node we encounter as we go if we arrive at problematic node, we apply the proper rotation to rebalance the tree

rebalancing

during a modifying operation of a binary tree, a node might become problematic, to restore balance to the tree so that it remains an AVL tree we use rotations

rotation

to determine which type of rotation we need to use to rebalance a given tree, we go 2 steps from the problematic node towards the newly inserted node which gives us the following 4 cases:

if we go 2 times to the left, then the rotation is of type LL
if we go 2 times to the right, then the rotation is of type RR
if we go left and then right then the rotation is of type LR
if we go right and then left then the rotation is of type RL

simple rotation

left left rotation

let z be the left child of the problematic node and x be the problematic node itself in Left Left rotation we rotate x to the right, such that the left child of x replaces x and x gets "rotated" to the right becoming the right child of z and a parent of the previous right child of z

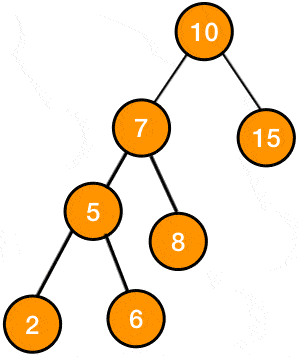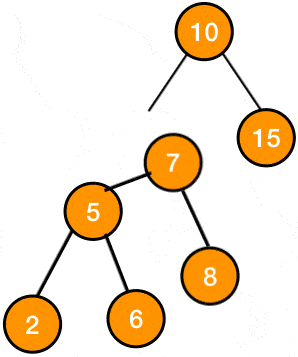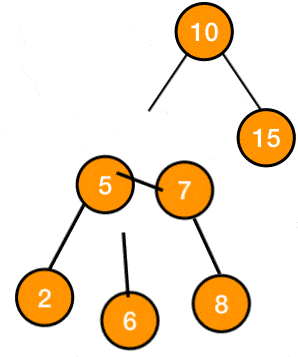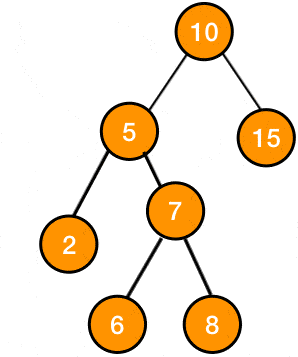
Figure 1: gif of left left rotation

consider the following AVL tree:

after inserting a new node with the value 2 this is how the tree would look:

the node with the value 7 whose balance factor is 2 is problematic because its causing imbalance in the tree, so we apply the rotation to its subtree to rebalance it

the subtree after the rotation:

and so the original tree would become:

right right rotation

this is very similar to Left Left, we first add the node and then if we have a problematic node x and if we took 2 steps to the right, then we use this rotation method this method consists of rotating the subtree such that x becomes a left child of its original right child z, and z takes the place of x and the previous left child of z becomes a right child of x at its new position

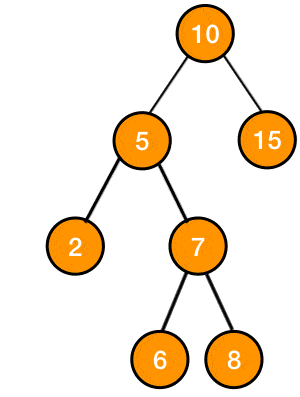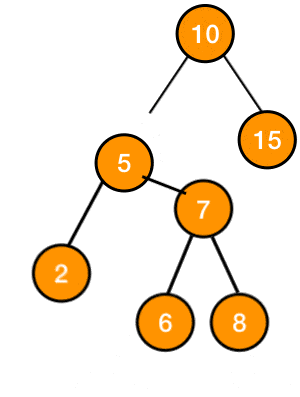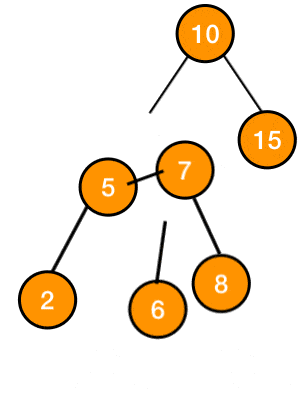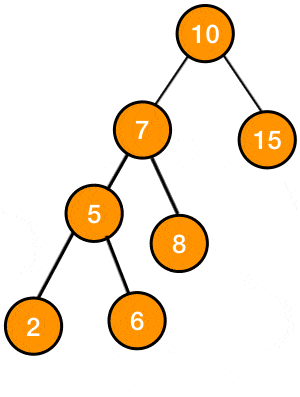
Figure 2: gif of right right rotation

double rotation

the difference between this and simple rotation is that this method consists of rotating twice as you might've already guessed from the title

left right rotation

this method consists of 2 steps, first is applying an RR rotation over the left child of the problematic node, then applying an LL rotation to the problematic node

right left rotation

this method consists of 2 steps, first is applying an LL rotation over the right child of the problematic node, then applying a RR rotation to the problematic node