cuda programming in common lisp

using cl-cuda.

load it using quicklisp:

(ql:quickload :cl-cuda)

arch linux setup

i had to install cuda for the nvcc compiler and more, and nvidia for the gpu driver, at first you may have to use /opt/cuda/bin/nvcc until you reboot or extend your $PATH.

to check which nvidia driver is in use run:

lspci -k | grep -A 2 -E "(VGA|3D)"

if you have installed the nvidia package and your os still uses nouveau you need to reboot. if it still doesnt use nvidia you need to update your while system with pacman -Syyu (you've been doing partial upgrades).

essential concepts

threads

mostly from https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#programming-model.

i also read the examples from the cl-cuda's source code.

kernels are just functions that are run by different cuda threads in a thread block, a thread block is a group of threads each given an index, thread blocks can be nested up to 3 times, an index is a 3d vector with each value corresponding to the index in one of the dimensions x,y,z, there is a limit to the number of threads per block, which on current GPUs is 1024. the index of a thread is stored in the special variable threadIdx, the index of a block is stored in the special variable blockIdx, the dimensions of a block can be given by blockDim, all of these variables are 3d vectors and have x,y,z members. a kernel can be executed by multiple equally-shaped thread blocks, so that the total number of threads is equal to the number of threads per block times the number of blocks.

blocks are organized into a one-dimensional, two-dimensional, or three-dimensional grid of thread blocks. the number of thread blocks in a grid is usually dictated by the size of the data being processed, which typically exceeds the number of processors in the system.

a thread block size of 16x16 (256 threads) is a common choice.

thread blocks are required to execute independently: it must be possible to execute them in any order, in parallel or in series. this independence requirement allows thread blocks to be scheduled in any order across any number of cores, enabling programmers to write code that scales with the number of cores.

threads within a block can cooperate by sharing data through some shared memory and by synchronizing their execution to coordinate memory accesses. more precisely, one can specify synchronization points in the kernel by calling the __syncthreads() intrinsic function; __syncthreads() acts as a barrier at which all threads in the block must wait before any is allowed to proceed. in addition to __syncthreads(), the cooperative groups api provides a rich set of thread-synchronization primitives.

for efficient cooperation, the shared memory is expected to be a low-latency memory near each processor core (much like an L1 cache) and __syncthreads() is expected to be lightweight.

memory

CUDA threads may access data from multiple memory spaces during their execution. each thread has private local memory. each thread block has shared memory visible to all threads of the block and with the same lifetime as the block. thread blocks in a thread block cluster can perform read, write, and atomics operations on each other’s shared memory. all threads have access to the same global memory.

there are also two additional read-only memory spaces accessible by all threads: the constant and texture memory spaces. the global, constant, and texture memory spaces are optimized for different memory usages. texture memory also offers different addressing modes, as well as data filtering, for some specific data formats.

the global, constant, and texture memory spaces are persistent across kernel launches by the same application.

unified memory provides managed memory to bridge the host and device memory spaces. managed memory is accessible from all CPUs and GPUs in the system as a single, coherent memory image with a common address space. this capability enables oversubscription of device memory and can greatly simplify the task of porting applications by eliminating the need to explicitly mirror data on host and device. the CUDA programming model also assumes that both the host and the device maintain their own separate memory spaces in DRAM, referred to as host memory and device memory, respectively. therefore, a program manages the global, constant, and texture memory spaces visible to kernels through calls to the CUDA runtime. this includes device memory allocation and deallocation as well as data transfer between host and device memory.

unified memory provides managed memory to bridge the host and device memory spaces. managed memory is accessible from all CPUs and GPUs in the system as a single, coherent memory image with a common address space. this capability enables oversubscription of device memory and can greatly simplify the task of porting applications by eliminating the need to explicitly mirror data on host and device.

device memory

the CUDA programming model assumes a system composed of a host and a device, each with their own separate memory. kernels operate out of device memory, so the runtime provides functions to allocate, deallocate, and copy device memory, as well as transfer data between host memory and device memory.

device memory can be allocated either as linear memory or as CUDA arrays.

CUDA arrays are opaque memory layouts optimized for texture fetching.

linear memory is allocated in a single unified address space, which means that separately allocated entities can reference one another via pointers, for example, in a binary tree or linked list. the size of the address space depends on the host system (CPU) and the compute capability of the used GPU.

code

see connect to remote common lisp repl with sly/slime for connecting to a remote common lisp repl with emacs.

notice that when working cl-cuda the data that we're passing to the gpu is gonna be duplicated (because its a binding from cl to C and uses whats called foreign memory), i never considered how bad that is, atleast in this case, as mostly when doing gpu calculations we're ofcourse passing lots of data and then copying it back, and the maximum amount of memory that i can use is already cut in half, if i have 16gb of memory i already know i cant use more than 8gb of that, thats pretty horrible (assuming i have a gpu with ~16gb memory), i can have my way around this, e.g. free memory from sbcl as it gets copied to C, but that'd be much more complexity than i wanna have to deal with

cuda vector addition

we start with the vectorAdd example, a simple example in C, stolen from https://github.com/NVIDIA/cuda-samples/blob/master/Samples/0_Introduction/vectorAdd/vectorAdd.cu and modified to reduce boilerplate code.

the syntax for calling a kernel in c++ is vector<<< blocks per grid, threads per block >>>(arg1,arg2,...).

consider the following program which does vector addition.

place this code in a file with a .cu extension (only .cu works):

#include <stdio.h>

__global__ void vector_add(float *c, float *a, float *b, int n) {
  for (int i = 0; i < n; i++) {
    c[i] = a[i] + b[i];
  }
}

int main() {
  const int N = 1000; // length of vectors
  size_t size = N * sizeof(float); // size of a vector in memory

  // allocate vectors in host memory
  float* host_a = (float*)malloc(size);
  float* host_b = (float*)malloc(size);
  float* host_c = (float*)malloc(size); // output vector a+b=c

  // initialize host input vectors
  for (int i = 0; i < N; i++) {
    host_a[i] = 1.0f;
    host_b[i] = 2.0f;
  }

  // allocate (global) linear memory for vectors on the device (gpu)
  float* device_a;
  float* device_b;
  float* device_c;
  cudaMalloc(&device_a, size);
  cudaMalloc(&device_b, size);
  cudaMalloc(&device_c, size);

  // copy vectors from host memory to device memory
  cudaMemcpy(device_a, host_a, size, cudaMemcpyHostToDevice);
  cudaMemcpy(device_b, host_b, size, cudaMemcpyHostToDevice);

  // invoke kernel
  int threads_per_block = 256;
  int blocks_per_grid =
    (N + threads_per_block - 1) / threads_per_block;
  vector_add<<<blocks_per_grid, threads_per_block>>>(device_c, device_b, device_a, N);

  // copy result from device memory to host memory
  cudaMemcpy(host_c, device_c, size, cudaMemcpyDeviceToHost);

  // free device memory
  cudaFree(device_a);
  cudaFree(device_b);
  cudaFree(device_c);

  for (int i = 0; i < N; ++i) {
    printf("%d: %f\n", i, host_c[i]);
  }

  // free host memory
  free(host_a);
  free(host_b);
  free(host_c);
}

compile with nvcc <name>.cu -o vector_add and run with ./vector_add.

similar same code but in cl:

(defun random-init (data n)
  (dotimes (i n)
    (setf (cl-cuda:memory-block-aref data i) (random 1.0))))

(cl-cuda:defkernel vec-add-kernel (cl-cuda:void ((a cl-cuda:float*) (b cl-cuda:float*) (c cl-cuda:float*) (n cl-cuda:int)))
  (let ((i (+ (* cl-cuda:block-dim-x cl-cuda:block-idx-x) cl-cuda:thread-idx-x)))
    (if (< i n)
        (set (aref c i)
             (+ (aref a i) (aref b i))))))

(defun main ()
  (let* ((dev-id 0)
         (n 1024)
         (threads-per-block 256)
         (blocks-per-grid (/ n threads-per-block)))
    (cl-cuda:with-cuda (dev-id)
      (cl-cuda:with-memory-blocks ((a 'float n) ;; allocate (global) linear memory on both host+device
                                   (b 'float n)
                                   (c 'float n))
        (random-init a n)
        (random-init b n)
        (cl-cuda:sync-memory-block a :host-to-device)
        (cl-cuda:sync-memory-block b :host-to-device)
        (vec-add-kernel a b c n
                        :grid-dim (list blocks-per-grid 1 1)
                        :block-dim (list threads-per-block 1 1))
        (cl-cuda:sync-memory-block c :device-to-host)
        (loop for i from 0 below 1024
              do (print (cl-cuda:memory-block-aref c i)))))))

cuda matrix multiplication

mostly taken from https://docs.nvidia.com/deeplearning/performance/dl-performance-matrix-multiplication/index.html and https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#programming-model.

before implementing matrix multiplication for the gpu we need to consider some things.

the product of two matrices results in a matrix which contains values, each of which is a dot product of K-element vectors. thus a total of fused multiply-adds are needed to compute the product. each FMA is 2 operations, a (scalar) multiplication and an addition, so a total of flops are required, if we were to consider gemm, the parameters would also play a role in the number of flops required, but the effect these scalars have can be negligable for sufficiently large matrices.

in the example of vector addition, we used global memory (using cudaMalloc in C and with-memory-block in CL), which is (very) slow compared to shared memory which is allocated per thread block. we also did one floating point operation per memory access, so with as many flops as we have you can already see how slow we are going. to speed this up we're gonna use shared memory so that threads in a thread block can collaborate in computing a submatrix of the output matrix and to reduce calls to global memory.

first, an implementation without shared memory:

#include <stdio.h>
#include <stdlib.h>

// matrices are stored in row-major order:
// M(row, col) = *(M.elements + row * M.width + col)
typedef struct {
  int width;
  int height;
  float* elements;
} Matrix;

// thread block size
#define BLOCK_SIZE 16

// forward declaration of the matrix multiplication kernel
__global__ void MatMulKernel(const Matrix, const Matrix, Matrix);

// matrix multiplication - host code
// matrix dimensions are assumed to be multiples of BLOCK_SIZE
void MatMul(const Matrix A, const Matrix B, Matrix C)
{
  // load A and B to device memory
  Matrix d_A;
  d_A.width = A.width; d_A.height = A.height;
  size_t size = A.width * A.height * sizeof(float);
  cudaMalloc(&d_A.elements, size);
  cudaMemcpy(d_A.elements, A.elements, size,
             cudaMemcpyHostToDevice);
  Matrix d_B;
  d_B.width = B.width; d_B.height = B.height;
  size = B.width * B.height * sizeof(float);
  cudaMalloc(&d_B.elements, size);
  cudaMemcpy(d_B.elements, B.elements, size,
             cudaMemcpyHostToDevice);

  // allocate C in device memory
  Matrix d_C;
  d_C.width = C.width; d_C.height = C.height;
  size = C.width * C.height * sizeof(float);
  cudaMalloc(&d_C.elements, size);

  // invoke kernel
  dim3 dimBlock(BLOCK_SIZE, BLOCK_SIZE);
  dim3 dimGrid(B.width / dimBlock.x, A.height / dimBlock.y);
  MatMulKernel<<<dimGrid, dimBlock>>>(d_A, d_B, d_C);

  // read C from device memory
  cudaMemcpy(C.elements, d_C.elements, size,
             cudaMemcpyDeviceToHost);

  // free device memory
  cudaFree(d_A.elements);
  cudaFree(d_B.elements);
  cudaFree(d_C.elements);
}

// matrix multiplication kernel called by MatMul()
__global__ void MatMulKernel(Matrix A, Matrix B, Matrix C)
{
  // each thread computes one element of C
  // by accumulating results into Cvalue
  float Cvalue = 0;
  int row = blockIdx.y * blockDim.y + threadIdx.y;
  int col = blockIdx.x * blockDim.x + threadIdx.x;
  for (int e = 0; e < A.width; ++e)
    Cvalue += A.elements[row * A.width + e]
      * B.elements[e * B.width + col];
  C.elements[row * C.width + col] = Cvalue;
}

int main() {
  Matrix a,b,c;
  // width*height should be a multiple of 16
  float elements[16*16];
  c.width = c.height = a.width = a.height = b.width = b.height = 16;
  a.elements = b.elements = elements;
  c.elements = (float*)malloc(sizeof(float)*c.width*c.height);
  for (int i = 0; i < c.width * c.height; ++i) {
    a.elements[i] = b.elements[i] = c.elements[i] = i;
  }
  MatMul(a,b,c);
  for (int i = 0; i < c.width * c.height; ++i) {
    printf("%f\n", c.elements[i]);
  }
}

to divide the work with shared memory we load submatrices into each thread block so that threads of each block can operate on the respective submatrix.

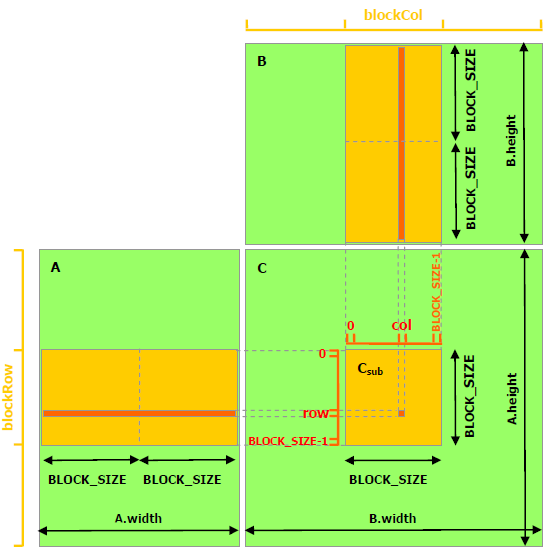the threads cooperate in loading from memory the values of the input matrices to minimize access to global memory, different thread blocks load different portions of the input matrices, the portions they load are exactly the part of the matrices needed to find the values of the submatrix of C they operate on.

the best way to understand this is to read the code:

// matrices are stored in row-major order:
// M(row, col) = *(M.elements + row * M.stride + col)
typedef struct {
  int width;
  int height;
  int stride;
  float* elements;
} Matrix;

// get a matrix element
__device__ float GetElement(const Matrix A, int row, int col) {
  return A.elements[row * A.stride + col];
}

// set a matrix element
__device__ void SetElement(Matrix A, int row, int col, float value) {
  A.elements[row * A.stride + col] = value;
}
// get the BLOCK_SIZExBLOCK_SIZE sub-matrix Asub of A that is
// located col sub-matrices to the right and row sub-matrices down
// from the upper-left corner of A
__device__ Matrix GetSubMatrix(Matrix A, int row, int col) {
  Matrix Asub;
  Asub.width    = BLOCK_SIZE;
  Asub.height   = BLOCK_SIZE;
  Asub.stride   = A.stride;
  Asub.elements = &A.elements[A.stride * BLOCK_SIZE * row
                              + BLOCK_SIZE * col];
  return Asub;
}

// thread block size
#define BLOCK_SIZE 16

// forward declaration of the matrix multiplication kernel
__global__ void MatMulKernel(const Matrix, const Matrix, Matrix);

// matrix multiplication - host code
// matrix dimensions are assumed to be multiples of BLOCK_SIZE
void MatMul(const Matrix A, const Matrix B, Matrix C) {
  // load A and B to device memory
  Matrix d_A;
  d_A.width = d_A.stride = A.width; d_A.height = A.height;
  size_t size = A.width * A.height * sizeof(float);
  cudaMalloc(&d_A.elements, size);
  cudaMemcpy(d_A.elements, A.elements, size,
             cudaMemcpyHostToDevice);
  Matrix d_B;
  d_B.width = d_B.stride = B.width; d_B.height = B.height;
  size = B.width * B.height * sizeof(float);
  cudaMalloc(&d_B.elements, size);
  cudaMemcpy(d_B.elements, B.elements, size,
             cudaMemcpyHostToDevice);

  // allocate C in device memory
  Matrix d_C;
  d_C.width = d_C.stride = C.width; d_C.height = C.height;
  size = C.width * C.height * sizeof(float);
  cudaMalloc(&d_C.elements, size);

  // invoke kernel
  dim3 dimBlock(BLOCK_SIZE, BLOCK_SIZE);
  dim3 dimGrid(B.width / dimBlock.x, A.height / dimBlock.y);
  MatMulKernel<<<dimGrid, dimBlock>>>(d_A, d_B, d_C);

  // read C from device memory
  cudaMemcpy(C.elements, d_C.elements, size,
             cudaMemcpyDeviceToHost);

  // free device memory
  cudaFree(d_A.elements);
  cudaFree(d_B.elements);
  cudaFree(d_C.elements);
}

// matrix multiplication kernel called by MatMul()
__global__ void MatMulKernel(Matrix A, Matrix B, Matrix C) {
  // block row and column
  int blockRow = blockIdx.y;
  int blockCol = blockIdx.x;
  // each thread block computes one sub-matrix Csub of C
  Matrix Csub = GetSubMatrix(C, blockRow, blockCol);
  // each thread computes one element of Csub
  // by accumulating results into Cvalue
  float Cvalue = 0;
  // thread row and column within Csub
  int row = threadIdx.y;
  int col = threadIdx.x;
  // loop over all the sub-matrices of A and B that are
  // required to compute Csub
  // multiply each pair of sub-matrices together
  // and accumulate the results
  for (int m = 0; m < (A.width / BLOCK_SIZE); ++m) {
    // get sub-matrix Asub of A
    Matrix Asub = GetSubMatrix(A, blockRow, m);
    // get sub-matrix Bsub of B
    Matrix Bsub = GetSubMatrix(B, m, blockCol);
    // shared memory (static variables) used to store Asub and Bsub respectively
    __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
    __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];
    // load Asub and Bsub from device memory to shared memory
    // each thread loads one element of each sub-matrix
    As[row][col] = GetElement(Asub, row, col);
    Bs[row][col] = GetElement(Bsub, row, col);
    // synchronize to make sure the sub-matrices are loaded
    // before starting the computation
    __syncthreads();
    // multiply Asub and Bsub together
    for (int e = 0; e < BLOCK_SIZE; ++e)
      Cvalue += As[row][e] * Bs[e][col];
    // synchronize to make sure that the preceding
    // computation is done before loading two new
    // sub-matrices of A and B in the next iteration
    __syncthreads();
  }
  // write Csub to device memory
  // each thread writes one element
  SetElement(Csub, row, col, Cvalue);
}

some points to consider before implementating in lisp:

we cant pass structs like in C, unfortunately, we can only allocate linear memory of basic types,
for matrices on cpu, i used cl's arrays, for matrices on gpu, im gonna use just C pointers, like in the C example,
common lisp implementation will be more complete (i cba doing the same for C), e.g. no assumptions on matrix sizes,
loops in kernels can only be done using the do statement.

(defun random-init (data n)
  (dotimes (i n)
    (setf (cl-cuda:memory-block-aref data i) (random 1.0))))

(cl-cuda:defkernel matrix-mul-kernel (cl-cuda:void ((arr1      cl-cuda:float*)
                                                    (arr2      cl-cuda:float*)
                                                    (out       cl-cuda:float*)
                                                    (arr1-rows cl-cuda:int)
                                                    (arr2-cols cl-cuda:int)
                                                    (arr2-rows cl-cuda:int)))
  (let* ((block-row cl-cuda:block-idx-y) ;; location of current thread block in the grid
         (block-col cl-cuda:block-idx-x)
         (row cl-cuda:thread-idx-y) ;; cell this thread is responsible for in output matrix
         (col cl-cuda:thread-idx-x)
         (c-value 10.0)
         (arr1-cols arr2-rows)
         (block-size cl-cuda:block-dim-x) ;; 16 unless modified
         (out-size arr1-rows))
    ;; start iterating through input submatrices
    ;; (set c-value (float arr1-cols))
    (do ((i 0 (+ i 1)))
        ((>= i (/ arr1-cols block-size)))
      (cl-cuda:with-shared-memory ((arr1-sub float 16 16)
                                   (arr2-sub float 16 16))
        (set (aref arr1-sub row col) (aref arr1 (+ (* block-row block-size)
                                                   (* row block-size)
                                                   (* i block-size)
                                                   col)))
        (set (aref arr2-sub row col) (aref arr2 (+ (* i block-size)
                                                   (* row block-size)
                                                   (* block-col block-size)
                                                   col)))
        (cl-cuda:syncthreads) ;; synchronize to make sure submatrices are loaded
        (do ((j 0 (+ j 1)))
            ((>= j block-size))
          (set c-value (+ c-value (* (aref arr1-sub row j) (aref arr2-sub j col)))))
        ;; synchronize to make sure that the preceding
        ;; computation is done before loading two new
        ;; sub-matrices of A and B in the next iteration
        (cl-cuda:syncthreads)))
    (set (aref out (+ (* block-row block-size)
                      (* block-col block-size)
                      (* row block-size)
                      col)) c-value)))

(defun cuda-matrix-mul (arr1 arr2)
  (let* ((out-size (* (array-rows arr1) (array-cols arr2)))
         (dev-id 0)
         (block-size 16) ;; actual size is squared, this is more of a "length"
         (threads-per-block (expt block-size 2))
         (blocks-per-grid (/ out-size threads-per-block)))
    (cl-cuda:with-cuda (dev-id)
      (cl-cuda:with-memory-blocks ((c-arr1 'float (array-size arr1))
                                   (c-arr2 'float (array-size arr2))
                                   (c-out 'float out-size))
        (random-init c-arr1 (array-size arr1))
        (random-init c-arr2 (array-size arr2))
        (cl-cuda:sync-memory-block c-arr1 :host-to-device)
        (cl-cuda:sync-memory-block c-arr2 :host-to-device)
        (matrix-mul-kernel
         c-arr1 c-arr2 c-out
         (array-rows arr1) (array-cols arr2) (array-rows arr2)
         :grid-dim (list blocks-per-grid 1 1)
         :block-dim (list block-size block-size 1))
        (cl-cuda:sync-memory-block c-out :device-to-host)))))

(defun example-cuda-matrix-mul ()
  (let ((size (expt 16 3)))
    (let ((mat1 (make-array (list size size) :initial-element 10))
          (mat2 (make-array (list size size) :initial-element 20)))
      (cuda-matrix-mul mat1 mat2))))

that took some effort, i had to hard-code the block size because as it compiles to C the variable isnt defined as a constant which it has to be because i'd get this error if i were to replace the number 16 with the variable block-size:

nvcc exits with code: 1
/tmp/cl-cuda.EjtQeE.cu(60): error: expression must have a constant value
                        __attribute__((shared)) float arr1_sub[block_size][block_size];

kernels are very limtied in terms of functionality, not everything can be used in kernels, almost everything is translated to C.

now a small benchmark to test this against my previous cpu solution:

(defun example-cuda-matrix-mul ()
  (let ((size (expt 16 3)))
    (let ((mat1 (make-array (list size size) :initial-element 10))
          (mat2 (make-array (list size size) :initial-element 20)))
      (cuda-matrix-mul mat1 mat2))))

(defun example-cpu-matrix-mul ()
  (let ((size 768))
    (let ((mat1 (make-array (list size size) :initial-element 10))
          (mat2 (make-array (list size size) :initial-element 20)))
      (matrix-mul mat1 mat2))))

(time (example-cuda-matrix-mul))
;; Evaluation took:
;;   2.776 seconds of real time
;;   2.771769 seconds of total run time (2.600099 user, 0.171670 system)
;;   [ Run times consist of 0.032 seconds GC time, and 2.740 seconds non-GC time. ]
;;   99.86% CPU
;;   7,192,807,350 processor cycles
;;   268,435,488 bytes consed

(time (example-cpu-matrix-mul))
;; Evaluation took:
;;   6.533 seconds of real time
;;   6.530840 seconds of total run time (6.530840 user, 0.000000 system)
;;   99.97% CPU
;;   16,934,213,216 processor cycles
;;   14,155,824 bytes consed

the values dont even scale linearly, the gpu version is much faster, a benchmark figure here would be a good idea but im too lazy to bother with that atm.