Table of Contents
- KeyValue
- lists
- stack
- queue
- tree
- heap
- hash table
- theorems
- average time complexity table
for most data structures i hadnt implemented deletion.
also its good to note that most of the code isnt optimized to hell, but it doesnt really matter since its only for educational purposes and you should probably be using the data structures provided by the programming language's standard library.
a data structure is a collection of data and operations on said data, the data is represented as objects, and each object x has:
key(x): a key that is used to identify the object (usually a number that uniquely identifies the object)info(x)orvalue(x): contains the data needed to store for the object (usually without the key)
for example, if x is a person, key(x) could be the person's ID, value(x) would be information on said person, like age, height, weight etc..
KeyValue
a helper class that represents a key-value/pair relation, used as a building block for many data structures
template <typename K, typename V> class KeyValue { private: K key; V value; public: KeyValue(K key, V value) { this->key = key; this->value = value; } K get_key() { return this->key; } V get_value() { return this->value; } void set_value(V value) { this->value = value; } void set_key(K key) { this->key = key; } friend bool operator <(const KeyValue<K, V>& c1, const KeyValue<K, V>& c2) { return c1.key < c2.key; } friend bool operator >(const KeyValue<K, V>& c1, const KeyValue<K, V>& c2) { return c1.key > c2.key; } };
lists
a list is an abstract data type that is a dynamically sized (often automatically resized) list of objects that stores as many objects as necessary, each type of list has its own method of dynamic storage.
in lists, ordering matters, and duplicate items may be allowed, unlike in sets.
linked list
a linked list is a concrete data type that is an implementation of a list
characteristics
- is the list sorted? the nodes are sorted by their
key(usually in an ascending order) - is the list doubly/singly linked? in a doubly linked list each node points to the next and previous node whereas in a singly linked list a node only points to the next
- does the list have a tail? a pointer
tail(x)points to the last node in a linked list - is the list circular? in a circular linked list the last node points to the first whereas in a non-circular linked list it points to NULL (nothing)
functions
insert(x): insertsxsearch(k): returns the node whose key iskisEmpty(): returns whether list is emptydelete(x): given the nodex, removes it from the list
implementation (c++)
Node
#include <cassert> template <typename T> class Node : public KeyValue<int, T> { private: Node<T>* next; public: Node(int key, T value) : KeyValue<int, T>(key, value) {} Node(int key) : KeyValue<int, T>(key, key) {} Node<T>* get_next() { return this->next; } void set_next(Node<T>* next) { assert(this != next); this->next = next; } bool has_next() { return this->next != nullptr; } Node<T>* get_tail() { Node<T>* n; for (n = this; n->get_next() != nullptr; n = n->get_next()); return n; } };
example usage:
#include <iostream> int main() { Node<int> n(10); std::cout << n.get_key() << std::endl; }
10
DoublyNode
template <typename T> class DoublyNode { private: DoublyNode<T>* left = nullptr; DoublyNode<T>* right = nullptr; T data; public: DoublyNode(T data) { this->data = data; } ~DoublyNode() { delete left; delete right; } T get_data() { return this->data; } void set_left(DoublyNode<T> node) { this->left = node; if (this->left != nullptr) { this->left->parent = this; } } void set_right(DoublyNode<T> node) { this->right = node; if (this->right != nullptr) { this->right->parent = this; } } DoublyNode<T> get_right() { return this->right; } DoublyNode<T> get_left() { return this->left; } bool has_right() { return this->right != nullptr; } bool has_left() { return this->left != nullptr; } };
LinkedList
template <typename T> class LinkedList { private: Node<T>* head; public: LinkedList() : head(nullptr) {} ~LinkedList() { Node<T>* n = this->head; while (n) { Node<T>* next = n->get_next(); delete n; n = next; } } Node<T>* get_head() { return this->head; } void set_head(Node<T>* n) { this->head = n; } LinkedList* add(int key) { return this->add(new Node<T>(key)); } LinkedList* add(Node<T>* n) { if (this->is_empty()) { this->head = n; } else { this->get_tail()->set_next(n); } return this; } Node<T>* get_tail() { if (this->is_empty()) return nullptr; return this->head->get_tail(); } bool is_empty() { return this->head == nullptr; } Node<T>* get_node(int index) { Node<T>* n = head; for (int i = 0; i < index; ++i) { n = n->get_next(); } return n; } int size() { Node<T>* n; int i = 0; for (n = this->head; n != nullptr; n = n->get_next()) { ++i; } return i; } };
example usage:
#include <iostream> int main() { LinkedList<int> l; for (int i = 0; i < 10; ++i) { l.add(20*(i+2)); } for (int i = 0; i < 5; ++i) { std::cout << l.get_node(i)->get_key() << std::endl; } }
40 60 80 100 120
DoublyLinkedList
to be implemented
LinkedListWithTail
to be implemented
CircularLinkedList
to be implemented
array list
an array list is a concrete data type that is an implementation of a list based on an array that is dynamically reconstructed on insertions to hold as many objects as necessary
some might suggest that an array list should shrink automatically aswell on deletions, though that isnt a popular implementation
an array list contains a fixed-size array initialized to a constant length, when the array gets filled we create a new array whose size is
where
is a constant (usually 2), and
is the previous size of the array, and we copy all the objects to the new array and then we have more space to store more objects
ArrayList
#include <cassert> #include <memory> #define INITIAL_SIZE 3 #define SCALING_FACTOR 2 template <typename T> class ArrayList { private: int actual_size; int idx; T* arr; T* allocate_memory(int num_of_objects) { this->actual_size = num_of_objects; // return new T[num_of_objects]; // return alloc.allocate(num_of_objects); return (T*)::operator new(num_of_objects * sizeof(T)); } void resize() { int prev_size = this->actual_size; T* newArr = allocate_memory(this->actual_size * SCALING_FACTOR); for (int i = 0; i < idx; ++i) { newArr[i] = this->arr[i]; } // delete[] this->arr; // alloc.deallocate(this->arr, prev_size); ::operator delete(this->arr); this->arr = newArr; } public: ArrayList() { this->idx = 0; this->arr = this->allocate_memory(INITIAL_SIZE); } ~ArrayList() { delete[] this->arr; } ArrayList<T>* add(T val) { if (this->idx == this->actual_size) this->resize(); this->arr[this->idx++] = val; return this; } T& get(int i) { return this->arr[i]; } T& operator [](int i) { return this->arr[i]; } void set(int index, T obj) { this->arr[index] = obj; } int size() { return this->idx; } void remove(int index) { assert(index < this->idx); for (int i = index; i < this->idx-1; ++i) { this->arr[i] = this->arr[i+1]; } this->idx--; } void insert(int index, T value) { assert(index < idx); if (idx == this->actual_size-1) this->resize(); for (int i = idx; i > index; --i) this->arr[i] = this->arr[i-1]; this->arr[index] = value; idx++; } static ArrayList<T>* from_array(T* other_arr, int length) { ArrayList<T>* list = new ArrayList<T>(); for (int i = 0; i < length; ++i) { list->add(other_arr[i]); } return list; } };
example usage:
#include <iostream> int main() { ArrayList<int> list; for (int i = 0; i < 3; ++i) { list.add(i*10)->add(i+2); } std::cout << "size is " << list.size() << std::endl; for (int i = 0; i < list.size(); ++i) { std::cout << list[i] << std::endl; } }
size is 6 0 2 10 3 20 4
stack
a stack is an abstract data type
queue
a queue is a linear abstract data type in which the operations are performed based on FIFO principle
tree
a tree is an abstract data type which stores data in the shape of a downwards-growing tree and every entry is called a node
node
trees store data as nodes, meaning each item in a tree is called a node
each node x has the following fields
key(x): a key that's used to identify the node (like every data structure)info(x): contains the data we need to store (like every data structure)left(x): a pointer to the left child ofxright(x): a pointer to the right childparent(x)(optional): a pointer to the parent ofx
every node in a binary tree has from 0 to 2 children
height
the height of a node x is defined as the height of subtree of said node, denoted by
balance factor
the balance factor of a node x, denoted by balance(x) or BF(x), is defined as the height of the subtree of the left child of x, denoted by
minus the height of the subtree of the right child of x denoted by
, in short:
see for example this tree, the balance factor of each node is written above it
height
the height of a tree is the number of the nodes in the longest path downwards (including the root node)
level
the level of a row in the tree is its distance from the root whose level is 1
root
the tree itself T (not for every node) contains a pointer root(T) that points to the root node of the tree (the first and topmost node)
leaf
a node that doesnt have children is called a leaf
internal node
a node that has atleast one child is called an internal node
sibling
2 nodes are considered siblings if they share the same parent node
ancestor
an ancestor of a given node is a node that is at an upper level of it
descendant
a descendant of a given node is a node that is at a lower level of the given node
subtree
for some binary tree T and a node x of said tree we denote
as the subtree whose root is x, and the left subtree of x is the tree whose root is the left child of x denoted by
and the right subtree of x is the tree whose root is the right child of x denoted by
the height of this tree is 4
complete tree
a complete binary tree is a binary tree in which every node has 2 or 0 children, and the leaves are all on at the same level
almost complete tree
an almost complete binary tree is a binary tree from which 0 or more nodes have been deleted continuously from the right part of the last level of nodes
the nodes in the last level in an almost complete binary tree have to appear continuously from left to right
every complete tree is an almost complete tree but not every almost complete tree is a complete tree
every level contains 2 times as many nodes as the level before it, except perhaps for the last level
the height of a tree is
the number of nodes in a tree is
the number of nodes at height
is
tree breadth-first search
breadth-first search or BFS for short, explores each level before moving onto the next one
extra memory, usually a queue, is needed to keep track of the child nodes that were encountered but not yet explored.
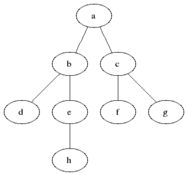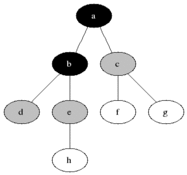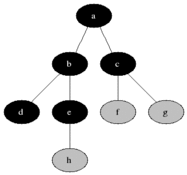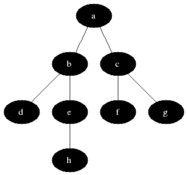
tree depth-first search
depth-first search or DFS for short, consists of exploring branches as far as possible before backtracking and exploring branches of other nodes
this is the algorithm we'll be using because its simpler
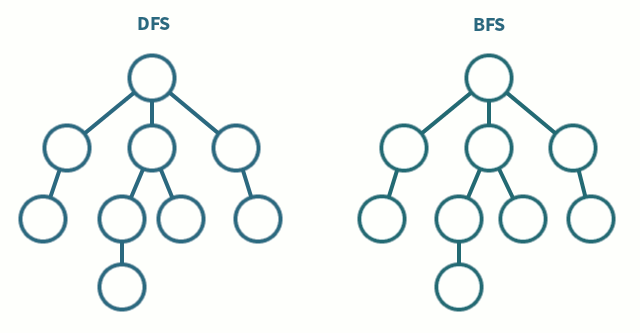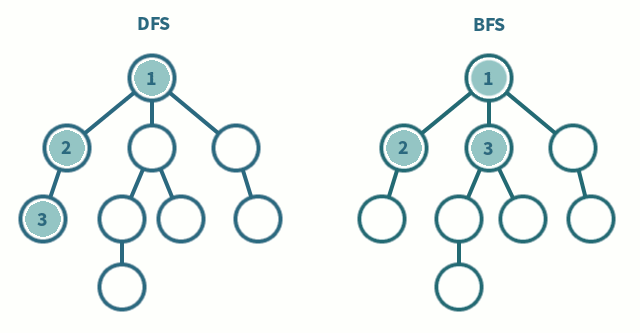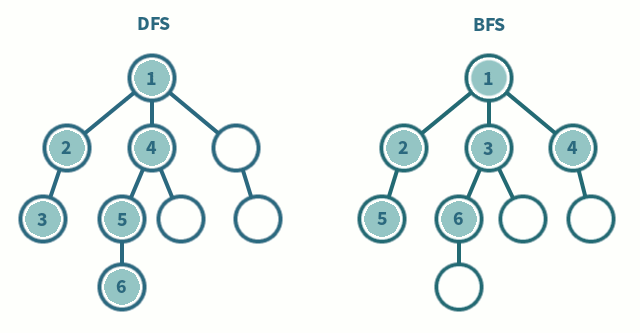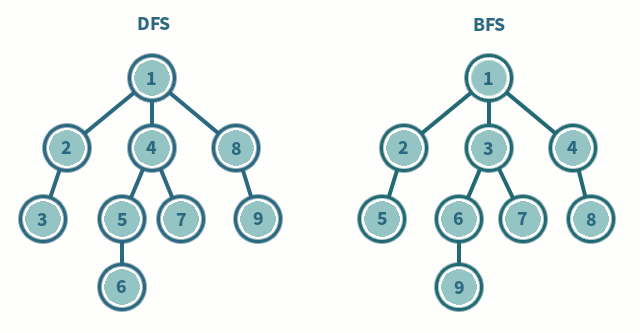
inorder traversal
left, parent, right
Algorithm inorder(tree) 1. go to the left child, i.e., call inorder(left-child), print it 2. go back to the parent, print it 3. go to the right child, i.e., call inorder(right-child), print it
note that before printing a child will always call inorder(left-child), so the first node to print would be the leftmost node in the deepest level
preorder traversal
parent, left, right
Algorithm preorder(tree) 1. visit the parent, print it 2. go to the left child, i.e., call preorder(left-child), print it 3. go to the right child, i.e., call preorder(right-child), print it
postorder traversal
left, right, parent
Algorithm postorder(tree) 1. go to the left child, i.e., call postorder(left-child), print it 2. go to the right child, i.e., call postorder(right-child), print it 3. visit the parent, print it
algorithms
reverse inorder
given a binary tree, write a function to reverse its inorder traversal output
this algorithm runs in O(n) time
template <typename T> void reverse(BinaryTreeNode<T>* node) { if (node == nullptr) return; reverse(node->get_left()); reverse(node->get_right()); BinaryTreeNode<T>* l = node->get_left(); node->set_left(node->get_right()); node->set_right(l); }
example usage:
#include <iostream> int main() { BinarySearchTree<int> t; t.insert(11)->insert(5)->insert(3)->insert(4)->insert(2)->insert(1)->insert(7)->insert(6)->insert(20)->insert(15); t.print(); reverse(t.get_root()); t.print(); }
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 11 | 15 | 20 |
| 20 | 15 | 11 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
binary tree
a binary tree is a concrete data type that is an implementation of a tree
BinaryTreeNode
#include <cstdlib> template <typename T> class BinaryTree; /* forward declare the class instead of including it */ template <typename T> class BinaryTreeNode { private: BinaryTreeNode<T>* parent; BinaryTreeNode<T>* right; BinaryTreeNode<T>* left; T value; int key; public: BinaryTreeNode(int key, T value) { this->key = key; this->value = value; this->parent = nullptr; this->right = nullptr; this->left = nullptr; } BinaryTreeNode(int key) { this->key = key; this->value = key; this->parent = nullptr; this->right = nullptr; this->left = nullptr; } ~BinaryTreeNode() { delete this->right; delete this->left; } void set_parent(BinaryTreeNode<T>* node) { this->parent = node; } void set_right(BinaryTreeNode<T>* node) { this->right = node; if (node != nullptr) node->parent = this; } void set_left(BinaryTreeNode<T>* node) { this->left = node; if (node != nullptr) node->parent = this; } BinaryTreeNode<T>* get_parent() { return this->parent; } BinaryTreeNode<T>* get_right() { return this->right; } BinaryTreeNode<T>* get_left() { return this->left; } bool has_right() { return this->right != nullptr; } bool has_left() { return this->left != nullptr; } bool has_parent() { return this->parent != nullptr; } T get_value() { return this->value; } int get_key() { return this->key; } bool is_leaf() { return !(this->has_left() || this->has_right()); } bool is_right_child() { return this->parent != nullptr && this->parent->get_right() == this; } bool is_left_child() { return this->parent != nullptr && this->parent->get_left() == this; } int height() { int right_height = this->has_left() ? this->get_left()->height() : 0; int left_height = this->has_right() ? this->get_right()->height() : 0; if (left_height > right_height) { return 1 + left_height; } return 1 + right_height; } BinaryTreeNode<T>* find(int key) { if (this->key == key) { return this; } BinaryTreeNode<T>* n_left = this->has_left() ? this->get_left()->find(key) : nullptr; BinaryTreeNode<T>* n_right = this->has_right() ? this->get_right()->find(key) : nullptr; return n_left != nullptr ? n_left : n_right; } int balance_factor() { if (this->has_left()) { if (this->has_right()) { return this->get_left()->height() - this->get_right()->height(); } else { return this->get_left()->height(); } } if (this->has_right()) { return 0 - this->get_right()->height(); } return 0; } bool is_balanced() { bool is_left_balanced = this->has_left() ? this->get_left()->is_balanced() : true; bool is_right_balanced = this->has_right() ? this->get_right()->is_balanced() : true; return !this->is_problematic() && is_left_balanced && is_right_balanced; } bool is_problematic() { return abs(this->balance_factor()) > 1; } BinaryTreeNode<T>* find_problematic_node() { if (this->is_problematic()) return this; BinaryTreeNode<T>* p_left = nullptr; BinaryTreeNode<T>* p_right = nullptr; if (this->has_left()) p_left = this->get_left()->find_problematic_node(); if (this->has_right()) p_right = this->get_right()->find_problematic_node(); return p_left == nullptr ? p_right : p_left; } bool is_complete(BinaryTreeNode<T>* root) { if (this->is_leaf()) return this->distance_to(root) == root->height(); if (!this->has_right() || !this->has_left()) return false; return this->right->is_complete(root) && this->left->is_complete(root); } int distance_to(BinaryTreeNode<T>* other) { if (other->height() > this->height()) { return other->find_path(this)->height(); } return this->find_path(other)->height(); } BinaryTreeNode<T>* find_path(BinaryTreeNode<T>* other) { if (this == other) { return new BinaryTreeNode<T>(other->key, other->value); } else { if (this->has_left()) { BinaryTreeNode<T>* n_left = this->get_left()->find_path(other); if (n_left != nullptr) { BinaryTreeNode<T>* node = new BinaryTreeNode<T>(this->key, this->value); node->set_left(n_left); return node; } } if (this->has_right()) { BinaryTreeNode<T>* n_right = this->get_right()->find_path(other); if (n_right != nullptr) { BinaryTreeNode<T>* node = new BinaryTreeNode<T>(this->key, this->value); node->set_right(n_right); return node; } } } return nullptr; } BinaryTreeNode<T>* find_rightmost_leaf() { if (this->is_leaf() && this->level() == this->find_root()->height()) { return this; } BinaryTreeNode<T>* from_right = this->has_right() ? this->get_right()->find_rightmost_leaf() : nullptr; if (from_right != nullptr) return from_right; return this->has_left() ? this->get_left()->find_rightmost_leaf() : nullptr; } BinaryTreeNode<T>* find_leftmost_leaf() { if (this->is_leaf() && this->level() == this->find_root()->height() - 1) { return this; } BinaryTreeNode<T>* from_left = this->has_left() ? this->get_left()->find_leftmost_leaf() : nullptr; if (from_left != nullptr) return from_left; return this->has_right() ? this->get_right()->find_leftmost_leaf() : nullptr; } bool has_right_and_left() { return this->has_left() && this->has_right(); } bool is_right() { return this->parent->get_right() == this; } bool is_left() { return this->parent->get_left() == this; } BinaryTreeNode<T>* get_right_uncle() { return this->parent->parent->right; } int level() { int lvl = 1; BinaryTreeNode<T>* n = this; while (n->has_parent()) { lvl++; n = n->get_parent(); } return lvl; } BinaryTreeNode<T>* find_root() { BinaryTreeNode<T>* n = this; while (n->has_parent()) { n = n->get_parent(); } return n; } void print() { if (this->has_left()) this->left->print(); std::cout << this->key << " "; if (this->has_right()) this->right->print(); } };
BinaryTree
template <typename T> class BinaryTree { private: BinaryTreeNode<T>* root; public: BinaryTree() { root = nullptr; } BinaryTree(BinaryTreeNode<T>* root) { this->root = root; } ~BinaryTree() { delete this->root; } BinaryTreeNode<T>* get_root() { return this->root; } void set_root(BinaryTreeNode<T>* node) { this->root = node; } bool is_empty() { return this->root == nullptr; } int size() { BinaryTreeNode<T>* n; int i = 0; for (n = this->get_root(); n != nullptr; n = n->get_right()) { ++i; } return i; } int height() { if (this->is_empty()) return 0; return this->root->height(); } bool is_balanced() { if (this->is_empty()) { return true; } return this->get_root()->is_balanced(); } BinaryTreeNode<T>* find_problematic_node() { return this->root->find_problematic_node(); } BinaryTreeNode<T>* find(int key) { return this->root->find(key); } /* inorder print */ void print() { if (!this->is_empty()) this->get_root()->print(); std::cout << "\n"; } void empty() { delete this->root; this->root = nullptr; } BinaryTree<T>* insert_right(BinaryTreeNode<T>* node) { if (this->is_empty()) { this->set_root(node); return this; } BinaryTreeNode<T>* n = this->get_root(); while (n->has_right()) { n = n->get_right(); } n->set_right(node); return this; } BinaryTree<T>* insert_left(BinaryTreeNode<T>* node) { if (this->is_empty()) { this->set_root(node); return this; } BinaryTreeNode<T>* n = this->get_root(); while (n->has_left()) { n = n->get_left(); } n->set_left(node); return this; } BinaryTree<T>* insert_right(int key) { return this->insert_right(new BinaryTreeNode<int>(key)); } BinaryTree<T>* insert_left(int key) { return this->insert_left(new BinaryTreeNode<int>(key)); } bool is_complete() { return this->is_empty() || this->root->is_complete(this->root); } /* note that this function gets the rightmost leaf in the last level */ BinaryTreeNode<T>* find_rightmost_leaf() { return this->root->find_rightmost_leaf(); } /* note that this function gets the leftmost leaf in the second-to-last level */ BinaryTreeNode<T>* find_leftmost_leaf() { return this->root->find_leftmost_leaf(); } };
the following code is used to print code that is rendered by latex to generate tree diagrams:
#include <iostream> template <typename T> void print_latex_forest_recurse(BinaryTreeNode<T>* node, bool print_value=false) { if (node == nullptr) return; if (print_value) std::cout << "[" << node->get_value() << ",circle,draw"; else std::cout << "[" << node->get_key() << ",circle,draw"; if (node->has_left()) { print_latex_forest_recurse(node->get_left(), print_value); } else { std::cout << "[,phantom]"; } if (node->has_right()) { print_latex_forest_recurse(node->get_right(), print_value); } else { std::cout << "[,phantom]"; } std::cout << "]"; } template <typename T> void print_latex_forest(BinaryTreeNode<T>* node, bool print_value=false) { // std::cout << "#+begin_src latex :results file graphics :file (temp-file \"svg\")" << std::endl; // std::cout << "\\nopagecolor" << "\\begin{forest}"; std::cout << "\\begin{forest}"; print_latex_forest_recurse(node, print_value); std::cout << "\\end{forest}" << std::endl;// << "#+end_src" << std::endl; }
example usage:
#include <iostream> int main() { BinaryTreeNode<int>* my_root = new BinaryTreeNode<int>(10); BinaryTree<int> t(my_root); print_latex_forest(t.get_root()); }
algorithms
add to the class of a binary tree a function that takes in an integer
and checks if there is a node in the tree that contains exactly
descendants, it should run in
time
#include <iostream> bool node_descendants(BinaryTreeNode<int>* n, int k) { if (n->is_leaf()) { return k == 0; } int new_num = k; if (n->has_right()) new_num--; if (n->has_left()) new_num--; if (n->has_right() && node_descendants(n->get_right(), new_num)) return true; if (n->has_left() && node_descendants(n->get_left(), new_num)) return true; if (n->has_right() && node_descendants(n->get_right(), k)) return true; if (n->has_left() && node_descendants(n->get_left(), k)) return true; return false; } int main() { t.print(); print_latex_forest(t.get_root()); std::cout << node_descendants(t.get_root(), 9) << std::endl; }
1 2 3 4 5 6 7 11 12 13 14 15 16 17 20 24 26
0
this code runs in
time
binary search tree
BinarySearchTree
template <typename T> class BinarySearchTree : public BinaryTree<T> { public: BinarySearchTree() {} BinarySearchTree(BinaryTreeNode<T>* node) : BinaryTree<T>(node) {} virtual BinarySearchTree<T>* insert(BinaryTreeNode<T>* node) { node->set_right(nullptr); node->set_left(nullptr); if (this->is_empty()) { BinaryTree<T>::set_root(node); } else { BinaryTreeNode<T>* n = this->get_root(); while (true) { if (node->get_key() < n->get_key()) { if (!n->has_left()) { n->set_left(node); node->set_parent(n); break; } n = n->get_left(); } else { if (!n->has_right()) { n->set_right(node); node->set_parent(n); break; } n = n->get_right(); } } } return this; } BinarySearchTree<T>* insert(int key, T value) { return this->insert(new BinaryTreeNode<T>(key, value)); } BinarySearchTree<T>* insert(int value) { return this->insert(new BinaryTreeNode<T>(value)); } BinarySearchTree<T>* insert(int* values, unsigned int size) { for (int i = 0; i < size; ++i) this->insert(new BinaryTreeNode<T>(values[i])); return this; } /* this needs to be implemented asap */ void remove(BinaryTreeNode<T>* node) { /* in case that node is the only one in the tree */ if (this->get_root()->is_leaf() && this->get_root() == node) { this->set_root(nullptr); return; } /* in case the node has no children */ BinaryTreeNode<T>* parent = node->get_parent(); if (node->is_leaf()) { if (node->is_right_child()) { parent->set_right(nullptr); } else { parent->set_left(nullptr); } } } void rotate_right(BinaryTreeNode<T>* node) { BinaryTreeNode<T>* previous_left = node->get_left(); if (node->is_left_child()) { node->get_parent()->set_left(previous_left); } else if (node->is_right_child()) { node->get_parent()->set_right(previous_left); } else if (node == this->get_root()) { this->set_root(previous_left); previous_left->set_parent(nullptr); } node->set_parent(previous_left); node->set_left(previous_left->get_right()); previous_left->set_right(node); } void rotate_left(BinaryTreeNode<T>* node) { BinaryTreeNode<T>* previous_right = node->get_right(); if (node->is_right_child()) { node->get_parent()->set_right(previous_right); } else if (node->is_left_child()) { node->get_parent()->set_left(previous_right); } else if (node == this->get_root()) { this->set_root(previous_right); previous_right->set_parent(nullptr); } node->set_parent(previous_right); node->set_right(previous_right->get_left()); previous_right->set_left(node); } };
example usage:
#include <iostream> int main() { BinarySearchTree<int> t; t.insert(11)->insert(5)->insert(3)->insert(4)->insert(2)->insert(1)->insert(7)->insert(6)->insert(20)->insert(15)->insert(24)->insert(16)->insert(12)->insert(14)->insert(13)->insert(17)->insert(26); std::cout << "is this tree balanced?: " << t.is_balanced() << std::endl; std::cout << "the height of this tree is: " << t.get_root()->height() << std::endl; std::cout << "the balance factor of the root is: " << t.get_root()->balance_factor() << std::endl; print_latex_forest(t.get_root()); BinaryTreeNode<int>* newroot = t.get_root()->find_path(t.find(13)); print_latex_forest(newroot); delete newroot; }
is this tree balanced?: 0
the height of this tree is: 6
the balance factor of the root is: -1
AVL tree
an AVL tree is a binary search tree in which every node x has a balance factor of
, meaning:
every node x of this tree holds an extra field called balance which holds the balance factor of said node
for example, the following tree is an AVL tree:
if we were to remove the node with value 14 or with value 9 this wouldnt be an AVL tree
let T be an AVL tree with n nodes and height
, then
minimal form
a minimal form of an AVL tree with a given height
is one which contains the least possible number of nodes
the minimal number of nodes for a tree of height
is given by the following recurrence relation
according to some sources, the base cases are
, but the base cases given above make more sense because a tree with a single node should have a height of 1 not 0
a minimal form of an AVL tree with a given number of nodes
is the one with the smallest height which is given by:
here is a python snippet to find the minimal number of nodes needed for a given height:
def find(height): if height == 1: return 1 if height == 2: return 2 return find(height-1) + find(height-2) + 1 return [(i,find(i)) for i in range(1,15)]
| height | nodes |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 7 |
| 5 | 12 |
| 6 | 20 |
| 7 | 33 |
| 8 | 54 |
| 9 | 88 |
| 10 | 143 |
| 11 | 232 |
| 12 | 376 |
| 13 | 609 |
| 14 | 986 |
problematic node
a problematic node is a node whose balance factor is
insertion
the process of inserting a node to an AVL tree starts with inserting it using the same insertion method we used for a binary search tree, after said insertion we start going up the tree starting at the new node we just inserted and updating the balance factor for every node we encounter as we go
if we arrive at problematic node, we apply the proper rotation to rebalance the tree
rebalancing
during a modifying operation of a binary tree, a node might become problematic, to restore balance to the tree so that it remains an AVL tree we use rotations
rotation
to determine which type of rotation we need to use to rebalance a given tree, we go 2 steps from the problematic node towards the newly inserted node which gives us the following 4 cases:
- if we go 2 times to the left, then the rotation is of type LL
- if we go 2 times to the right, then the rotation is of type RR
- if we go left and then right then the rotation is of type LR
- if we go right and then left then the rotation is of type RL
simple rotation
let z be the left child of the problematic node and x be the problematic node itself
in Left Left rotation we rotate x to the right, such that the left child of x replaces x and x gets "rotated" to the right becoming the right child of z and a parent of the previous right child of z
gif of left left rotation
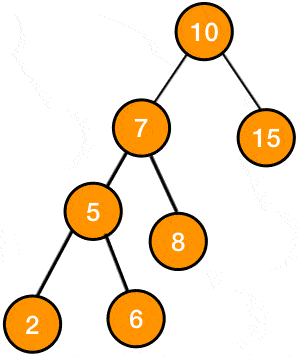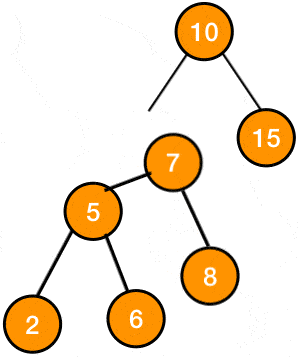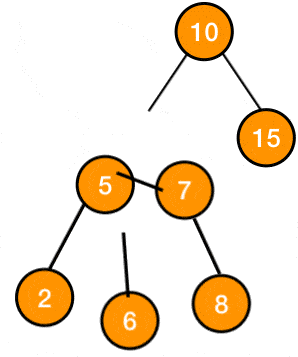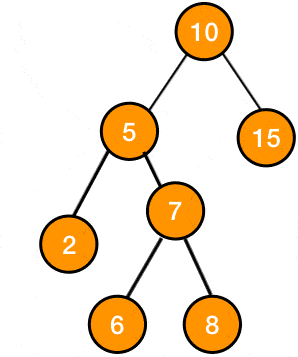
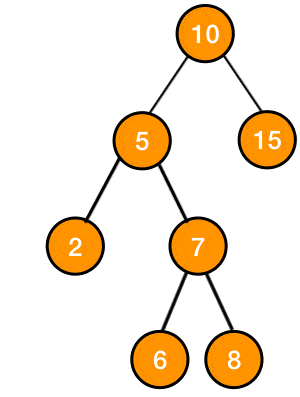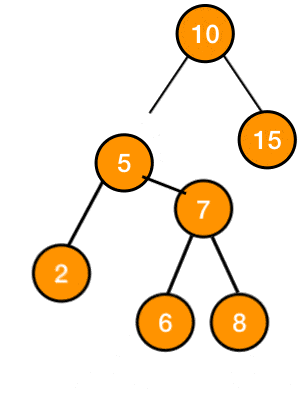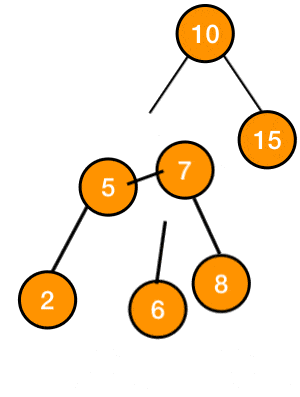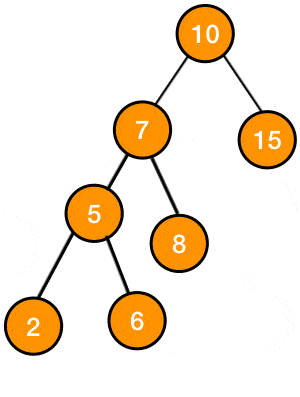
consider the following AVL tree:
after inserting a new node with the value 2 this is how the tree would look:
the node with the value 7 whose balance factor is 2 is problematic because its causing imbalance in the tree, so we apply the rotation to its subtree to rebalance it
the subtree after the rotation:
and so the original tree would become:
this is very similar to Left Left, we first add the node and then if we have a problematic node x and if we took 2 steps to the right, then we use this rotation method
this method consists of rotating the subtree
such that x becomes a left child of its original right child z, and z takes the place of x and the previous left child of z becomes a right child of x at its new position
gif of right right rotation
double rotation
the difference between this and simple rotation is that this method consists of rotating twice as you might've already guessed from the title
this method consists of 2 steps, first is applying an RR rotation over the left child of the problematic node, then applying an LL rotation to the problematic node
this method consists of 2 steps, first is applying an LL rotation over the right child of the problematic node, then applying a RR rotation to the problematic node
AVLTree
template <typename T> class AVLTree : public BinarySearchTree<T> { public: using BinarySearchTree<T>::insert; AVLTree() {} AVLTree(BinaryTreeNode<T>* node) : BinarySearchTree<T>(node) {} AVLTree<T>* insert(BinaryTreeNode<T>* node) override { BinarySearchTree<T>::insert(node); BinaryTreeNode<T>* retracing_node = node; while (retracing_node != nullptr) { if (retracing_node->is_problematic()) { BinaryTreeNode<T>* path_root = retracing_node->find_path(node); if (path_root->has_left() && path_root->get_left()->has_left()) { /* LL rotation */ this->rotate_right(retracing_node); } if (path_root->has_right() && path_root->get_right()->has_right()) { /* RR rotation */ this->rotate_left(retracing_node); } if (path_root->has_right() && path_root->get_right()->has_left()) { /* RL rotation */ this->rotate_right(retracing_node->get_right()); /* LL rotation */ this->rotate_left(retracing_node); /* RR rotation */ } if (path_root->has_left() && path_root->get_left()->has_right()) { /* LR rotation */ this->rotate_left(retracing_node->get_left()); /* RR rotation */ this->rotate_right(retracing_node); /* LL rotation */ } delete path_root; break; } retracing_node = retracing_node->get_parent(); } return this; } };
example:
#include <iostream> int main() { AVLTree<int> t; t.insert(11)->insert(5)->insert(3)->insert(4)->insert(2)->insert(1)->insert(7)->insert(6)->insert(20)->insert(15)->insert(24)->insert(16)->insert(12)->insert(14)->insert(13)->insert(17)->insert(26); print_latex_forest(t.get_root()); }
2-3 tree
a 2–3 tree is a tree concrete data type where every internal node is either a 2-node or 3-node
an exceptional case is when the tree contains only one element in which case the only node in the tree (which is the root) holds only one element
every internal node is a 2-node or a 3-node
all leaves are at the same level
keys are always ordered from left to right in ascending order
2-node
we say that an internal node is a 2-node if it holds one value and two children
3-node
we say that an internal node is a 3-node if it holds two values and three children
insertion
an important property to keep in mind is that insertion always occurs in one of the leaves
2-3 insertion visual explanation, from https://iq.opengenus.org/2-3-trees/
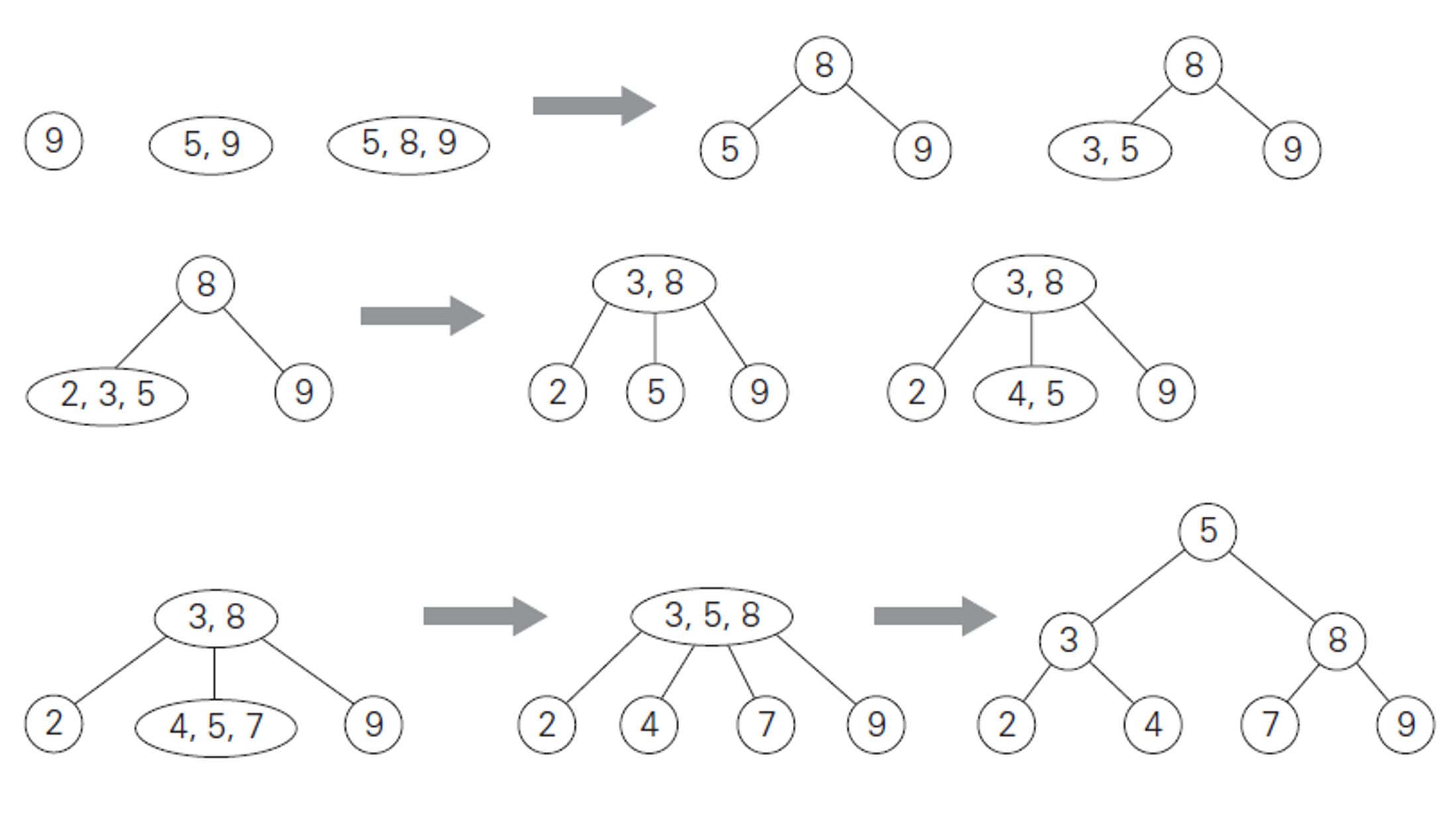
TwoThreeNode
const int SIZE = 3; template <typename T> class TwoThreeNode { private: TwoThreeNode<T>* parent; TwoThreeNode<T>* children[SIZE+1]; int keys[SIZE]; T values[SIZE]; public: void set_child(int idx, TwoThreeNode<T>* node) { this->children[idx] = node; if (node) node->parent = this; } TwoThreeNode<T>* get_child(int idx) { return this->children[idx]; } void remove_child(TwoThreeNode<T>* node) { for (int i = 0; i < SIZE; ++i) { if (this->children[i] == node) { this->children[i]->parent = nullptr; this->children[i] = nullptr; return; } } } int add_child(TwoThreeNode<T>* node) { for (int i = 0; i < SIZE; ++i) { if (this->keys[i] > node->biggest_key() || this->keys[i] == 0) { this->set_child(i, node); return i; } } this->set_child(SIZE, node); return SIZE; } int add_key_value(int key, T value) { for (int i = 0; i < SIZE; ++i) { if (this->keys[i] == 0) { this->keys[i] = key; this->values[i] = value; return i; } if (this->keys[i] > key) { this->children[SIZE] = this->children[SIZE-1]; for (int j = SIZE-1; j > i; --j) { this->keys[j] = this->keys[j-1]; this->values[j] = this->values[j-1]; this->children[j] = this->children[j-1]; } this->keys[i] = key; this->values[i] = value; return i; } } return -1; } void set_key(int idx, int key) { this->keys[idx] = key; } int get_key(int idx) { return this->keys[idx]; } bool has_key(int idx) { return this->keys[idx] != 0; } bool has_child(int idx) { return this->children[idx] != nullptr; } void set_value(int idx, T value) { this->values[idx] = value; } T get_value(int idx) { return this->values[idx]; } void set_parent(TwoThreeNode<T>* node) { this->parent = node; } TwoThreeNode<T>* get_parent() { return this->parent; } bool has_parent() { return this->parent != nullptr; } bool is_leaf() { for (int i = 0; i < SIZE; ++i) { if (children[i] != nullptr) return false; } return true; } bool is_root() { return !this->has_parent(); } TwoThreeNode<T>* find_node_to_place_key(int key) { if (this->is_leaf()) { for (int i = 0; i < SIZE; ++i) { if (this->keys[i] > key || this->keys[i] == 0) { return this; } } return nullptr; } for (int i = 0; i < SIZE; ++i) { if (this->keys[i] > key || this->keys[i] == 0) { return this->children[i]->find_node_to_place_key(key); } } return this->children[SIZE] == nullptr ? nullptr : this->children[SIZE]->find_node_to_place_key(key); } TwoThreeNode<T>* find_node_with_biggest_key() { if (this->is_leaf()) return this; TwoThreeNode<T>* biggest = nullptr; int biggest_key = 0; for (int i = 0; i < SIZE; ++i) { if (this->children[i] != nullptr) { TwoThreeNode<T>* tmp = this->children[i]->find_node_with_biggest_key(); if (tmp == nullptr) continue; for (int j = 0; j < tmp->count_keys(); ++j) { if (tmp->keys[j] > biggest_key) { biggest = tmp; biggest_key = tmp->keys[j]; } } } } return biggest; } int find_biggest_key() { if (this->is_leaf()) { return this->biggest_key(); } int biggest = this->biggest_key(); for (int i = 0; i < SIZE; ++i) { if (this->children[i] != nullptr) { int other = this->children[i]->find_biggest_key(); if (other > biggest) biggest = other; } } return biggest; } int find_smallest_key() { if (this->is_leaf()) { return this->smallest_key(); } int smallest = this->smallest_key(); for (int i = 0; i < SIZE; ++i) { if (this->children[i] != nullptr) { int other = this->children[i]->find_smallest_key(); if (other != 0 && other < smallest && other != -1) smallest = other; } } return smallest; } int biggest_key() { int biggest = 0; for (int i = 0; i < SIZE; ++i) { if (this->keys[i] > biggest) biggest = this->keys[i]; } return biggest; } int smallest_key() { int smallest = -1; for (int i = 0; i < SIZE; ++i) { if ((this->keys[i] < smallest && this->keys[i] != 0) || smallest == -1) smallest = this->keys[i]; } return smallest; } int count_keys() { int cnt = 0; for (int i = 0; i < SIZE; ++i) { if (this->keys[i] != 0) { ++cnt; } } return cnt; } int count_children() { int cnt = 0; for (int i = 0; i < SIZE; ++i) { if (this->children[i] != nullptr) { ++cnt; } } return cnt; } bool is_2_node() { return this->count_keys() == 1; } bool is_3_node() { return this->count_keys() == 2; } void print() { for (int i = 0; i < SIZE; ++i) { std::cout << this->keys[i] << " "; } std::cout << std::endl; } std::string to_string() { std::string str = ""; for (int i = 0; i < SIZE; ++i) { std::string num_str = this->keys[i] == 0 ? "\(\\varnothing\)" : std::to_string(this->keys[i]); str += num_str + (i == SIZE - 1 ? "" : " "); } return str; } int height() { if (this->is_leaf()) return 1; for (int i = 0; i < SIZE; ++i) { if (this->children[i] != nullptr) { return 1+this->children[i]->height(); } } return 1; } int get_left_key() { return this->keys[0]; } int get_right_key() { return this->keys[1]; } bool has_left_key() { return this->keys[0] != 0; } bool has_right_key() { return this->keys[1] != 0; } TwoThreeNode<T>* get_left_child() { return this->children[0]; } TwoThreeNode<T>* get_right_child() { return this->children[2]; } TwoThreeNode<T>* get_mid_child() { return this->children[1]; } bool has_left_child() { return this->children[0] != nullptr; } bool has_right_child() { return this->children[2] != nullptr; } bool has_mid_child() { return this->children[1] != nullptr; } };
TwoThreeTree
template <typename T> class TwoThreeTree { private: TwoThreeNode<T>* root = nullptr; public: TwoThreeNode<T>* get_root() { return this->root; } void add_key_value(int key, T value) { if (this->root == nullptr) { this->root = new TwoThreeNode<T>(); this->root->set_key(0, key); this->root->set_value(0, value); return; } TwoThreeNode<T>* node = this->root->find_node_to_place_key(key); if (node == nullptr) { node = this->root->find_node_with_biggest_key(); } std::cout << "adding key " << key << " to " << (node == nullptr ? "unknown" : node->to_string()) << std::endl; int key_count = node->count_keys(); if (key_count < SIZE-1) { std::cout << "added " << key << " to " << node->to_string() << " and got "; node->add_key_value(key, value); std::cout << node->to_string() << std::endl; return; } if (key_count >= SIZE-1) { node->add_key_value(key, value); std::cout << "balance " << node->to_string() << std::endl; balance(node); } } /* helping function */ void balance(TwoThreeNode<T>* node) { std::cout << "root: " << this->root->to_string() << std::endl; if (node->is_2_node() || node->is_3_node()) { std::cout << node->to_string() << " is good." << std::endl; return; } if (node->is_root()) { TwoThreeNode<T>* new_root = new TwoThreeNode<T>(); new_root->add_key_value(node->get_key(1), node->get_value(1)); TwoThreeNode<T>* new_left_node = new TwoThreeNode<T>(); TwoThreeNode<T>* new_right_node = new TwoThreeNode<T>(); new_left_node->set_key(0, node->get_key(0)); new_right_node->set_key(0, node->get_key(2)); new_left_node->set_child(0, node->get_child(0)); new_left_node->set_child(1, node->get_child(1)); new_right_node->set_child(0, node->get_child(2)); new_right_node->set_child(1, node->get_child(3)); new_root->set_child(0, new_left_node); new_root->set_child(1, new_right_node); std::cout << "created new root " << new_root->to_string() << " to replace " << this->root->to_string() << ", left child: " << new_left_node->to_string() << ", right child: " << new_right_node->to_string() << std::endl; this->root = new_root; return; } TwoThreeNode<T>* the_parent = node->get_parent(); std::cout << "adding " << node->get_key(1) << " to " << the_parent->to_string() << " to get "; the_parent->add_key_value(node->get_key(1), node->get_value(1)); std::cout << the_parent->to_string() << std::endl; node->set_key(1, 0); split(node); std::cout << "balance " << the_parent->to_string() << " recursively" << std::endl; balance(the_parent); delete node; } void split(TwoThreeNode<T>* node) { std::cout << "split " << node->to_string() << std::endl; TwoThreeNode<T>* the_parent = node->get_parent(); TwoThreeNode<T>* new_left_node = new TwoThreeNode<T>(); TwoThreeNode<T>* new_right_node = new TwoThreeNode<T>(); new_left_node->set_key(0, node->get_key(0)); new_right_node->set_key(0, node->get_key(2)); new_left_node->set_child(0, node->get_child(0)); new_left_node->set_child(1, node->get_child(1)); new_right_node->set_child(0, node->get_child(2)); new_right_node->set_child(1, node->get_child(3)); the_parent->remove_child(node); std::cout << "inserting right " << new_right_node->to_string() << " as a " << the_parent->add_child(new_right_node) << "th child of " << the_parent->to_string() << std::endl; //the_parent->add_child(new_right_node); std::cout << "inserting left " << new_left_node->to_string() << " as a " << the_parent->add_child(new_left_node) << "th child of " << the_parent->to_string() << std::endl; //the_parent->add_child(new_left_node); } bool is_empty() { return this->root == nullptr; } int height() { return this->is_empty() ? 0 : this->root->height(); } };
the following code is used to print code that is rendered by latex to generate two-three-tree tree diagrams:
#include <iostream> template <typename T> void print_latex_forest_twothree_tree_recurse(TwoThreeNode<T>* node, bool print_value=false) { if (node == nullptr) return; std::string one; std::string two; std::string three; if (print_value) { one = node->get_key(0) == 0 ? "\(\\varnothing\)" : std::to_string(node->get_value(0)); two = node->get_key(1) == 0 ? "\(\\varnothing\)" : std::to_string(node->get_value(1)); three = node->get_key(2) == 0 ? "\(\\varnothing\)" : std::to_string(node->get_value(2)); } else { one = node->get_key(0) == 0 ? "\(\\varnothing\)" : std::to_string(node->get_key(0)); two = node->get_key(1) == 0 ? "\(\\varnothing\)" : std::to_string(node->get_key(1)); three = node->get_key(2) == 0 ? "\(\\varnothing\)" : std::to_string(node->get_key(2)); } std::cout << "[\\nodepart{one} " << one << " \\nodepart{two} " << two << " \\nodepart{three} " << three; for (int i = 0; i < SIZE; ++i) { if (node->get_child(i) != nullptr) { print_latex_forest_twothree_tree_recurse(node->get_child(i), print_value); } else { // std::cout << "[,phantom]"; } } std::cout << "]"; } template <typename T> void print_latex_forest_twothree_tree(TwoThreeNode<T>* node, bool print_value=false) { // std::cout << "#+begin_src latex :results file graphics :file (temp-file \"svg\")" << std::endl; std::cout << "\\begin{dummyenv}\\forestset{rect/.style = {rectangle split, rectangle split horizontal, rectangle split parts=3, draw}}" << std::endl; std::cout << "\\nopagecolor" << "\\begin{forest} for tree={rect} "; print_latex_forest_twothree_tree_recurse(node, print_value); std::cout << "\\end{forest}\\end{dummyenv}" << std::endl;// << "#+end_src" << std::endl; }
example usage:
#include <iostream> int main() { TwoThreeTree<float> t; const float seq[] = {3,2,7,9,5,4,3.5,4.5,3.2,4.7,1,10,11,10.5,2.5,3.7,12}; for (int i = 0; i < 17; ++i) { t.add_key_value((int)(seq[i]*10), seq[i]); } print_latex_forest_twothree_tree(t.get_root()); }
adding key 20 to 30
added 20 to 30
and got 20 30
adding key 70 to 20 30
balance 20 30 70
root: 20 30 70
created new root 30
to replace 20 30 70, left child: 20
, right child: 70
adding key 90 to 70
added 90 to 70
and got 70 90
adding key 50 to 70 90
balance 50 70 90
root: 30
adding 70 to 30
to get 30 70
split 50
90
inserting right 90
as a 2th child of 30 70
inserting left 50
as a 1th child of 30 70
balance 30 70
recursively
root: 30 70
30 70
is good.
adding key 40 to 50
added 40 to 50
and got 40 50
adding key 35 to 40 50
balance 35 40 50
root: 30 70
adding 40 to 30 70
to get 30 40 70
split 35
50
inserting right 50
as a 2th child of 30 40 70
inserting left 35
as a 1th child of 30 40 70
balance 30 40 70 recursively
root: 30 40 70
created new root 40
to replace 30 40 70, left child: 30
, right child: 70
adding key 45 to 50
added 45 to 50
and got 45 50
adding key 32 to 35
added 32 to 35
and got 32 35
adding key 47 to 45 50
balance 45 47 50
root: 40
adding 47 to 70
to get 47 70
split 45
50
inserting right 50
as a 1th child of 47 70
inserting left 45
as a 0th child of 47 70
balance 47 70
recursively
root: 40
47 70
is good.
adding key 10 to 20
added 10 to 20
and got 10 20
adding key 100 to 90
added 100 to 90
and got 90 100
adding key 110 to 90 100
balance 90 100 110
root: 40
adding 100 to 47 70
to get 47 70 100
split 90
110
inserting right 110
as a 3th child of 47 70 100
inserting left 90
as a 2th child of 47 70 100
balance 47 70 100 recursively
root: 40
adding 70 to 40
to get 40 70
split 47
100
inserting right 100
as a 2th child of 40 70
inserting left 47
as a 1th child of 40 70
balance 40 70
recursively
root: 40 70
40 70
is good.
adding key 105 to 110
added 105 to 110
and got 105 110
adding key 25 to 10 20
balance 10 20 25
root: 40 70
adding 20 to 30
to get 20 30
split 10
25
inserting right 25
as a 1th child of 20 30
inserting left 10
as a 0th child of 20 30
balance 20 30
recursively
root: 40 70
20 30
is good.
adding key 37 to 32 35
balance 32 35 37
root: 40 70
adding 35 to 20 30
to get 20 30 35
split 32
37
inserting right 37
as a 3th child of 20 30 35
inserting left 32
as a 2th child of 20 30 35
balance 20 30 35 recursively
root: 40 70
adding 30 to 40 70
to get 30 40 70
split 20
35
inserting right 35
as a 1th child of 30 40 70
inserting left 20
as a 0th child of 30 40 70
balance 30 40 70 recursively
root: 30 40 70
created new root 40
to replace 30 40 70, left child: 30
, right child: 70
adding key 120 to 105 110
balance 105 110 120
root: 40
adding 110 to 100
to get 100 110
split 105
120
inserting right 120
as a 2th child of 100 110
inserting left 105
as a 1th child of 100 110
balance 100 110
recursively
root: 40
100 110
is good.
heap
a heap is an abstract data type
min heap
a min heap is a heap in which each node is less than or equal to both its children
max heap
a max heap is a heap in which each node is bigger than or equal to both its children
binary heap
A binary heap is defined as a binary tree with two additional constraints:
- shape property: a binary heap is an almost complete tree
- heap property: the key stored in each node is either greater than or equal to, or less than or equal to the keys in the node's children
a heap may keep a pointer to speed up insertion, this pointer points to the leftmost leaf if the tree is complete, otherwise if its almost complete, it points to the right uncle of the rightmost leaf
in a heap the keys arent necessarily sorted like in binary search trees
bubbling
moving a node up/down a heap to get it to its correct position
bubble up
bubbling a node upwards consists of recursively switching it with its parent until its parent is bigger/smaller than it (depending on whether we're using a min heap or a max heap)
bubble down
bubbling a node downards consists of recursively switching it with one of its children until it gets to its correct position
this is a pseudocode for the algorithm:
l = left(i) // index of left child r = right(i) // index of right child if l <= heap-size[A] and A[l] > A[i] largest = l else largest = i if r <= heap-size[A] and A[r] > A[largest] largest = r if largest != i exchange A[i] A[largest] heapify(A, largest)
time complexity is
insertion
inserting a new node to the heap consists of adding it as a leaf such that the heap remains almost complete and bubbling up the newly added node so that the keys in the tree remain sorted
if the heap is in array representation, we insert the new node to the end of the array and heapify it upwards (bubble up)
deletion
deletion of a node consists of replacing the rightmost leaf with it and bubble it downwards if its smaller than one of its children or upwards if its bigger than its parent
binary heap array representation
some resources may use assume that arrays start at index 1, i see no point in that since most programming languages use 0 as the first index, so some of the following propositions might seem a little different like for example the proposition number 2 in the following list according to these sources would be that the left child of i^{th} node is
instead of
and the right child is
for an array to represent a binary heap, the only condition is that
(in the case of max heap)
arrays that represent heap have the following characterstics:
- root is
- the parent of the i^{th} node (in the array) is
- left child of the i^{th} node is
- right child of the i^{th} node is
in other words, the nodes are taken from the root to the last level from left to right and put in that order in an array
the array should hold 2 values, array-size, which is the size of the array, and heap-size, which is the number of elements of the heap in the array
construction of binary heap from array
given some random array, e.g. A=[10,20,30,40,50,70,35,60,80], we need to reorganize its elements such that it represents a binary heap
to achieve this we apply bubble down to the first half of the array in reverse (because the leaf nodes need not be heapified as they already follow the heap property)
e.g. for the given array we apply bubble(A, i) such that
this is the constructing algorithm in pseudocode:
Build-Heap(A) n = length(A) heap-size = n for i = n/2 to 1 heapify(A, i)
this algorithm runs in
time
for
we know:
so for
:
to be continued
binary heap algorithms
biggest k nodes
initial inefficient solution:
we analyze the time complexity of this algorithm:
which means that the time complexity is
we cant arrive at Big Theta for this algorithm
we suggest another algorithm that is more efficient:
BinaryHeap
this is a max heap implementation
#include <cmath> #define PARENT_INDEX(node_idx) floor((node_idx-1)/2) #define LEFT_CHILD_INDEX(node_idx) 2*node_idx+1 #define RIGHT_CHILD_INDEX(node_idx) 2*node_idx+2 template <typename T> class BinaryHeap { private: ArrayList<KeyValue<int, T>>* list = new ArrayList<KeyValue<int, T>>(); // heapify downwards assuming max heap void heapify_down(int idx) { KeyValue<int, T>* current = &this->list->get(idx); KeyValue<int, T>* left = LEFT_CHILD_INDEX(idx) >= list->size() ? nullptr : &this->list->get(LEFT_CHILD_INDEX(idx)); KeyValue<int, T>* right = RIGHT_CHILD_INDEX(idx) >= list->size() ? nullptr : &this->list->get(RIGHT_CHILD_INDEX(idx)); if (left == nullptr && right == nullptr) return; if (left == nullptr) { if (right->get_key() > current->get_key()) { KeyValue<int, T> temp = *current; this->list->set(idx, *right); this->list->set(RIGHT_CHILD_INDEX(idx), temp); heapify_down(RIGHT_CHILD_INDEX(idx)); } } else if (right == nullptr) { if (left->get_key() > current->get_key()) { KeyValue<int, T> temp = *current; this->list->set(idx, *left); this->list->set(LEFT_CHILD_INDEX(idx), temp); heapify_down(LEFT_CHILD_INDEX(idx)); } } else { if (left->get_key() > current->get_key() && left->get_key() > right->get_key()) { KeyValue<int, T> temp = *current; this->list->set(idx, *left); this->list->set(LEFT_CHILD_INDEX(idx), temp); heapify_down(LEFT_CHILD_INDEX(idx)); } if (right->get_key() > current->get_key() && right->get_key() > left->get_key()) { KeyValue<int, T> temp = *current; this->list->set(idx, *right); this->list->set(RIGHT_CHILD_INDEX(idx), temp); heapify_down(RIGHT_CHILD_INDEX(idx)); } } } void heapify_up(int idx) { if (idx == 0) return; KeyValue<int, T>* current = &this->list->get(idx); KeyValue<int, T>* parent = &this->list->get(PARENT_INDEX(idx)); if (current->get_key() > parent->get_key()) { KeyValue<int, T> temp = *current; this->list->set(idx, *parent); this->list->set(PARENT_INDEX(idx), temp); heapify_up(PARENT_INDEX(idx)); } } BinaryTreeNode<T>* to_binary_tree(int idx) { if (idx >= this->list->size()) return nullptr; BinaryTreeNode<T>* node = new BinaryTreeNode<T>(this->list->get(idx).get_key(), this->list->get(idx).get_value()); BinaryTreeNode<T>* left = to_binary_tree(LEFT_CHILD_INDEX(idx)); BinaryTreeNode<T>* right = to_binary_tree(RIGHT_CHILD_INDEX(idx)); node->set_left(left); node->set_right(right); return node; } public: ~BinaryHeap() { delete this->list; } BinaryHeap<T>* insert(KeyValue<int, T> kv) { this->list->add(kv); this->heapify_up(this->list->size()-1); return this; } BinaryHeap<T>* insert(int key) { return this->insert(KeyValue<int, int>(key, key)); } KeyValue<int, T>& operator [](int i) { return (*list)[i]; } KeyValue<int, T>& get(int i) { return (*list)[i]; } static BinaryHeap<T>* from_array(KeyValue<int, T>* other_arr, int length) { BinaryHeap<T>* heap = new BinaryHeap<T>(); heap->list = ArrayList<KeyValue<int, T>>::from_array(other_arr, length); for (int i = length / 2; i >= 0; --i) { heap->heapify_down(i); } return heap; } int size() { return this->list->size(); } BinaryTree<T>* to_binary_tree() { return new BinaryTree<T>(to_binary_tree(0)); } };
example usage:
#include <iostream> int main() { // KeyValue<int, int> arr[4] = {{11, 11}, {21, 21}, {31, 31}, {41, 41}}; // BinaryHeap<int>* h = BinaryHeap<int>::from_array(arr, 4); BinaryHeap<int> h; for (int i = 0; i < 10; ++i) { std::cout << "inserting " << i << std::endl; h.insert(i); BinaryTree<int>* bt = h.to_binary_tree(); print_latex_forest(bt->get_root()); delete bt; } }
inserting 0
inserting 1
inserting 2
inserting 3
inserting 4
inserting 5
inserting 6
inserting 7
inserting 8
inserting 9
check if array represents a binary heap
#include <iostream> template <typename HEAP> bool is_binary_heap(HEAP heap, int left, int right) { if (left > right) return true; if ((2*left <= right && heap[2*left+1] > heap[left]) || (2*left+2 <= right && heap[2*left+2] > heap[right])) return false; return is_binary_heap(heap, 2*left+1, right) && is_binary_heap(heap, 2*left+2, right); } int main() { BinaryHeap<int> h; for (int i = 0; i < 5; ++i) { h.insert(i); std::cout << i << std::endl; } std::cout << is_binary_heap(h, 0, 4) << std::endl; std::cout << is_binary_heap(new int[] {1,2,3,4,5}, 0, 4) << std::endl; }
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
binomial heap
BinomialHeapNode
template <typename T> class BinomialHeapNode : public Node<T> { private: BinomialHeapNode<T>* parent; BinomialHeapNode<T>* child; /* leftmost child */ /* right sibling is the field "next" of the parent class */ public: BinomialHeapNode(int key, T value) : Node<T>(key, value) {} BinomialHeapNode(int key) : Node<T>(key, key) {} BinomialHeapNode<T>* get_parent() { return this->parent; } BinomialHeapNode<T>* get_child() { return this->child; } void set_child(BinomialHeapNode<T>* node) { if (node != nullptr) node->set_parent(this); this->child = node; } void set_parent(BinomialHeapNode<T>* node) { this->parent = node; } bool has_child() { return this->child != nullptr; } bool is_root() { return this->parent == nullptr; } int degree() { BinomialHeapNode<T>* n = this; int degree = 0; for (n = this; n->get_child() != nullptr; n = n->get_child()) { degree++; } return degree; } };
BinomialHeap
template <typename T> class BinomialHeap { private: BinomialHeapNode<T>* head = nullptr; public: BinomialHeap() = default; BinomialHeap(BinomialHeapNode<T>* head) { this->head = head; } int order() { BinomialHeapNode<T>* tail = head->get_tail(); return tail->degree(); } bool is_empty() { return this->head == nullptr; } BinomialHeap<T>* insert(BinomialHeapNode<T>* node) { if (this->is_empty()) this->head = node; else this->unite(new BinomialHeap<T>(node)); return this; } BinomialHeapNode<T>* get_head() { return this->head; } void merge(BinomialHeap<T>* other) { BinomialHeapNode<T>* this_iterator = this->head; BinomialHeapNode<T>* n = other->head; while (n != nullptr) { while (this_iterator->has_next() && ((BinomialHeapNode<T>*)this_iterator->get_next())->degree() < n->degree()) this_iterator = (BinomialHeapNode<T>*)this_iterator->get_next(); BinomialHeapNode<T>* old_n_next = (BinomialHeapNode<T>*)n->get_next(); if (n->degree() < this->head->degree()) { n->set_next(this->head); this->head = n; this->head->set_parent(nullptr); /* TODO should reset child and parent */ } else { BinomialHeapNode<T>* old_this_next = (BinomialHeapNode<T>*)this_iterator->get_next(); this_iterator->set_next(n); n->set_next(old_this_next); } n = old_n_next; } } void unite(BinomialHeap<T>* other) { this->merge(other); BinomialHeapNode<T>* n = this->head; BinomialHeapNode<T>* prev = nullptr; while (n != nullptr && n->has_next()) { BinomialHeapNode<T>* next = (BinomialHeapNode<T>*)n->get_next(); BinomialHeapNode<T>* nextnext = n->has_next() ? (BinomialHeapNode<T>*)n->get_next()->get_next() : nullptr; bool next_same = next != nullptr && n->degree() == next->degree(); bool nextnext_same = nextnext != nullptr && n->degree() == nextnext->degree(); if (!next_same) { prev = n; n = (BinomialHeapNode<T>*)n->get_next(); // std::cout << "case 1" << std::endl; } else if (next_same && nextnext_same) { prev = n; n = (BinomialHeapNode<T>*)n->get_next(); // std::cout << "case 2" << std::endl; } else if (next_same && !nextnext_same && n->get_key() < next->get_key()) { // remove next and attach it to n // std::cout << "attaching " << next->get_key() << " to " << n->get_key() << std::endl; next->set_next(n->get_child()); n->set_next(nextnext); n->set_child(next); // std::cout << "case 3" << std::endl; } else if (next_same && !nextnext_same && n->get_key() > next->get_key()) { // remove n and attach it to next // std::cout << "attaching " << n->get_key() << " to " << next->get_key() << std::endl; BinomialHeapNode<T>* new_n = next; n->set_next(next->get_child()); if (prev != nullptr) { prev->set_next(next); } else { /* its the first root now */ this->head = next; } next->set_child(n); // std::cout << "case 4" << std::endl; n = new_n; } } } };
the following code is used to print code that is rendered by latex to generate binomial heap diagrams:
template <typename T> void print_latex_forest_recurse(BinomialHeapNode<T>* node, bool print_value=false) { if (node == nullptr) return; if (node->is_root()) { std::cout << "\\begin{forest} for tree={calign=last, circle, draw} [" << node->get_key() << ",baseline"; if (node->has_child()) { print_latex_forest_recurse((BinomialHeapNode<T>*)node->get_child(), print_value); } std::cout << "]"; std::cout << "\\end{forest}"; print_latex_forest_recurse((BinomialHeapNode<T>*)node->get_next(), print_value); } else { std::cout << "[" << node->get_key(); print_latex_forest_recurse((BinomialHeapNode<T>*)node->get_child(), print_value); std::cout << "]"; if (node->has_next()) { print_latex_forest_recurse((BinomialHeapNode<T>*)node->get_next(), print_value); } } } template <typename T> void print_latex_forest(BinomialHeapNode<T>* node, bool print_value=false) { // std::cout << "#+begin_src latex :results file graphics :file (temp-file \"svg\")" << std::endl; // std::cout << "\\nopagecolor"; print_latex_forest_recurse(node, print_value); std::cout << std::endl;// << "#+end_src" << std::endl; }
example usage:
#include <iostream> int main() { BinomialHeap<int> b; for (int i = 0; i < 15; ++i) { std::cout << "inserting " << i << std::endl; b.insert(new BinomialHeapNode<int>(i)); print_latex_forest(b.get_head()); } }
inserting 0
inserting 1
inserting 2
inserting 3
inserting 4
inserting 5
inserting 6
inserting 7
inserting 8
inserting 9
inserting 10
inserting 11
inserting 12
inserting 13
inserting 14
hash table
a hash table, is an abstract data type that maps keys to values. a hash table uses a hash function to compute an index into an array of buckets or slots, from which the desired value can be found. during lookup, the key is hashed and the resulting hash indicates where the corresponding value is stored.
it contains the following functions:
Insert(A, x)Delete(A, x)Search(A, x)
theorems
the number of nodes in a complete tree of height
is
we add all the nodes in a given complete tree according to their levels to get
the height of a complete tree with
nodes is
according to the previous lemma
, therefore
the number of leaves in a complete tree with
nodes and height
is
using induction
the base case is
, a complete tree of height 1 contains 1 node only which is a leaf, so
we assume the statement holds true for every
we prove the statements holds true for
, looking at a complete tree of height
, we can build it using a tree of height
by adding 2 children to every leaf, so
which means the statement holds true for
the number of leaves in a complete tree that holds
nodes is
we denote by
the height of the tree:
in an almost complete tree, the number of nodes in a specific level is 2 times the number of nodes in level before it (except for perhaps the last level)
the height of an almost complete tree with
nodes is
the number of leaves in an almost complete tree with
nodes is
the number of nodes with height
in an almost complete tree with
nodes is
for every almost complete tree with
nodes and height
,
the biggest almost complete tree of height
is a complete tree and so
the smallest almost complete tree of height
can be constructed by adding a left child to the leftmost leaf of a complete tree of height
,
for every almost complete tree with
nodes and height
,
for every almost complete tree with
nodes and height
,
average time complexity table
that
is usually but not necessarily equal to
(when talking about trees) as sometimes
see https://stackoverflow.com/questions/12258114/big-oh-vs-big-ologn-in-trees
| data structure | insert | search |
|---|---|---|
| linked list | ||
| array list | ||
| Hash table | ||
| binomial heap | ||
| binary heap | ||
| queue | ||
| stack | ||
| binary search tree | ||
| AVL tree | ||
| 2-3 tree |