yet another divide-and-conquer algorithm given an array, this algorithm keeps splitting it until it reaches a subarray that cant be divided which happens when a subarray contains only 1 or 0 elements, each of these subarrays are sorted individually and then combined, recursively, to eventually make a larger sorted array refer to merge algorithm this algorithm runs in time
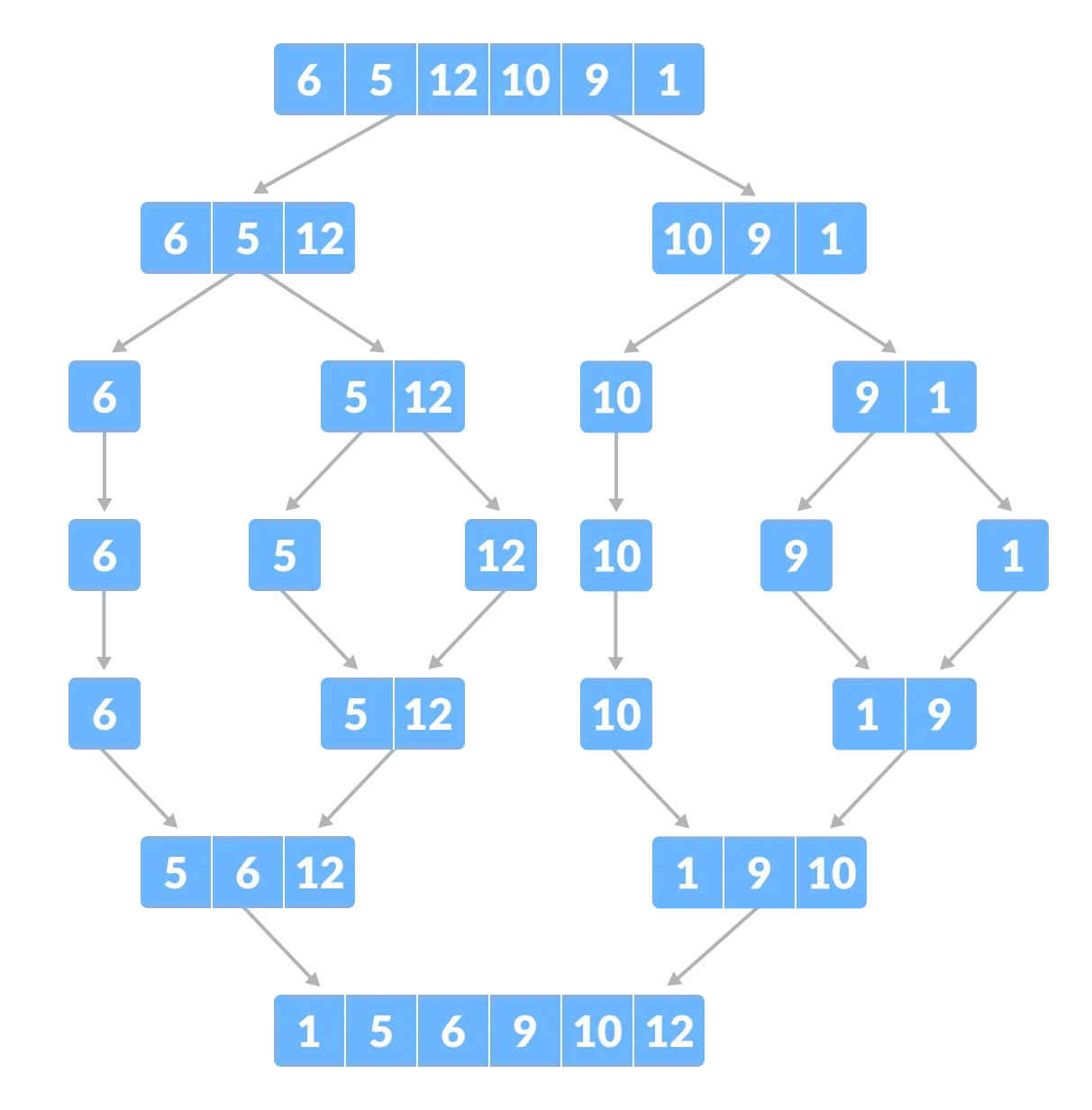
Figure 1: this image visualizes the process
#include <iostream> template <typename T> void merge(T arr[], int l, int m, int r) { int n1 = m - l + 1; int n2 = r - m; T L[n1]; T R[n2]; for (int i = 0; i < n1; ++i) L[i] = arr[l + i]; for (int j = 0; j < n2; ++j) R[j] = arr[m + 1 + j]; int i = 0, j = 0; int k = l; while (i < n1 && j < n2) { if (L[i] <= R[j]) arr[k++] = L[i++]; else arr[k++] = R[j++]; } while (i < n1) arr[k++] = L[i++]; while (j < n2) arr[k++] = R[j++]; } template <typename T> void sort(T arr[], int l, int r) { if (l < r) { int m = l+(r-l)/2; sort(arr, l, m); sort(arr, m + 1, r); merge(arr, l, m, r); } }